
【题目】选修![]() :坐标系与参数方程
:坐标系与参数方程
已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为![]() .
.
(Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换![]() 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
【答案】(1)(x﹣2)2+4y2=4, 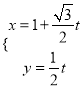 (2)
(2)![]()
【解析】试题分析:(Ⅰ)曲线![]() 的极坐标方程化为
的极坐标方程化为![]() ,利用
,利用![]() 能求出曲线
能求出曲线![]() 直角坐标方程;由直线
直角坐标方程;由直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,能求出直线
,能求出直线![]() 的参数方程;(Ⅱ)由曲线
的参数方程;(Ⅱ)由曲线![]() 经过伸缩变换
经过伸缩变换![]() ,后得到曲线
,后得到曲线![]() ,求出曲线
,求出曲线![]() 为:
为: ![]() ,把直线
,把直线![]() 的参数方程代入直线
的参数方程代入直线![]() ,得
,得![]() ,设
,设![]() 对应的参数分别为
对应的参数分别为![]() ,则
,则![]()
![]() ,由此能求出
,由此能求出![]() .
.
试题解析:(Ⅰ)∵曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,∴ρ2﹣4ρcosθ+3ρ2sin2θ=0,
∴曲线C的直角坐标方程为x2+y2﹣4x+3y2=0,整理,得(x﹣2)2+4y2=4,
∵直线l过点M(1,0),倾斜角为![]() ,
,
∴直线l的参数方程为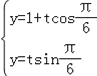 ,即
,即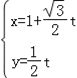 ,(t是参数).
,(t是参数).
(Ⅱ)∵曲线C经过伸缩变换![]() 后得到曲线C′,
后得到曲线C′,
∴曲线C′为:(x﹣2)2+y2=4,
把直线l的参数方程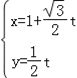 ,(t是参数)代入曲线C′:(x﹣2)2+y2=4,
,(t是参数)代入曲线C′:(x﹣2)2+y2=4,
得:![]() ,
,
设A,B对应的参数分别为t1,t2,则t1+t2=![]() ,t1t2=﹣3,
,t1t2=﹣3,
|MA|+|MB|=|t1|+|t2|=|t1﹣t2|=![]() =
=![]() =
=![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)=0.5x2-bx, (b为常数)。
(1)函数f(x)的图象在点(1,f(1))处的切线与函数g(x)的图象相切,求实数b的值;
(2)若函数h(x)=f(x)+g(x)在定义域上不单调,求实数b的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对函数”.现给出四个函数:
为“偏对函数”.现给出四个函数: 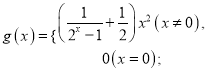
![]() ;
; ![]() . 则其中是“偏对称函数”的函数个数为( )
. 则其中是“偏对称函数”的函数个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中有7个大小、形状相同的小球,6个白球1个红球.现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取.试设计一个模拟试验,计算恰好第三次摸到红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
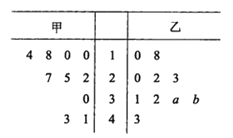
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当![]() 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为![]() ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为![]() ,比较
,比较![]() 的大小关系;
的大小关系;
(2)在这10个卖场中,随机选取2个卖场,记![]() 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若![]() ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com