【题目】（本小题满分13分）
如图，在正四面体
中，
分别是棱
的中点.
（1）求证：四边形
是平行四边形；
（2）求证：
平面；
（3）求证：
平面
.
【答案】见解析.
【解析】
试题分析：第一问应用三角形的中位线的性质，可知四边形的一组对边平行且相等的，从而根据平行四边形的判定定理，得出结果，对于第二问，注意把握线面平行的判定定理的内容，找准平行线即可，三角形的中位线是现成的，对于第三问，掌握线面垂直的判定定理的内容，找准两条相交直线与之垂直即可，正三角形的中线和垂线是重合的，好好写即可.
试题解析：
证明：（1）∵
分别是棱
的中点，
∴
，且
， （2分）
∴
且
， （3分）
∴四边形
是平行四边形. （4分）
（2）由（1）知，
， （5分）
且
平面，
平面， （7分）
∴
平面. （8分）
（3）∵
是正四面体，
所以它的四个面是全等的等边三角形. （9分）
∵ H是BC的中点，
∴
. （11分）
又SH平面SAH，AH平面SAH，且
，（12分）
∴
平面
. （13分）
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目：高中数学 来源： 题型：
【题目】下面给出四种说法：
①用相关指数R2来刻画回归效果，R2越小，说明模型的拟合效果越好；
②命题P：“x0∈R，x02﹣x0﹣1＞0”的否定是￢P：“x∈R，x2﹣x﹣1≤0”；
③设随机变量X服从正态分布N（0，1），若P（x＞1）=p则P（﹣1＜X＜0）=
﹣p
④回归直线一定过样本点的中心（
）．
其中正确的说法有（ ）
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2017届云南省云南师范大学附属中学高三高考适应性月考（五）文数】已知函数
.
（1）若曲线
在点
处的切线斜率为1，求函数
的单调区间；
（2）若
时，
恒成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.
有时可用函数
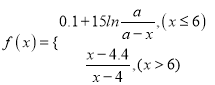
描述学习某学科知识的掌握程度，其中x表示某学科知识的学习次数（
），
表示对该学科知识的掌握程度，正实数a与学科知识有关.
（1） 证明：当
时，掌握程度的增加量
总是下降；
（2） 根据经验，学科甲、乙、丙对应的a的取值区间分别为
,
,
.当学习某学科知识6次时，掌握程度是85%，请确定相应的学科.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分14分）
已知动点M到点
的距离等于M到点
的距离的
倍.
（1）求动点M的轨迹C的方程；
（2）若直线
与轨迹C没有交点，求
的取值范围；
（3）已知圆
与轨迹C相交于
两点，求
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知椭圆
（a＞b＞0）的离心率
，过点
和
的直线与原点的距离为
．
（1）求椭圆的方程．
（2）已知定点
，若直线
与椭圆交于C、D两点．问：是否存在k的值，使以CD为直径的圆过E点?请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】四棱锥P﹣ABCD中，底面ABCD是边长为8的菱形，∠BAD=
，若PA=PD=5，平面PAD⊥平面ABCD．
（1）求四棱锥P﹣ABCD的体积；
（2）求证：AD⊥PB．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
