
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 底面
底面![]() ,且
,且![]() 在底面正投影点在线段
在底面正投影点在线段![]() 上,
上,![]() ,
,![]() .
.
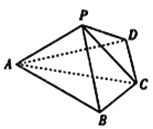
(1)证明:![]() ;
;
(2)若![]() ,
,![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求钝二面角
,求钝二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题(1)分析条件易得![]() 平面
平面![]() , ∵
, ∵![]() 平面
平面![]() , ∴
, ∴![]() ;
;
(2)作![]() 于点
于点![]() ,则
,则![]() 底面
底面![]() ,
, ![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 的方向分别为
的方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,分别求平面
,分别求平面![]() 和平面
和平面![]() 的法向量,用向量求解即可.
的法向量,用向量求解即可.
试题解析:
(1)如图,连接![]() 交
交![]() 于点
于点![]() .∵
.∵![]() ,即
,即![]() 为等腰三角形,又
为等腰三角形,又![]() 平分
平分![]() ,故
,故![]() ,∵平面
,∵平面![]() 底面
底面![]() , 平面
, 平面![]() 底面
底面![]() ,∴
,∴![]() 平面
平面![]() , ∵
, ∵![]() 平面
平面![]() ,
,
∴![]() .
.
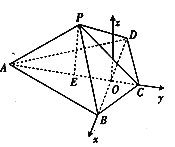
(2)作![]() 于点
于点![]() ,则
,则![]() 底面
底面![]() ,
, ![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 的方向分别为
的方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() .
.![]() ,而
,而![]() ,得
,得![]() ,
,
又![]() ,故
,故![]() .
.
设![]() ,则由
,则由![]() ,得
,得![]() ,而
,而![]() ,
,
由![]() ,得
,得![]() ,则
,则![]() ,
,
所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
由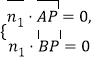 得
得![]() 可取
可取![]() ,
,
由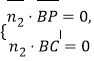 得
得![]() 可取
可取![]() ,
,
从而法向量![]() 的夹角的余弦值为
的夹角的余弦值为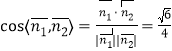 .
.
由图可知二面角![]() 是钝角,故二面角
是钝角,故二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,过
,过![]() 作与x轴垂直的直线与椭圆交于P,Q点,若|PQ|=
作与x轴垂直的直线与椭圆交于P,Q点,若|PQ|=![]() .
.
(1)求椭圆E的方程;
(2)设过![]() 的直线l的斜率存在且不为0,直线l交椭圆于A,B两点,若以AB为直径的圆过椭圆左焦点
的直线l的斜率存在且不为0,直线l交椭圆于A,B两点,若以AB为直径的圆过椭圆左焦点![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着支付宝、微信等支付方式的上线,越来越多的商业场景可以实现手机支付.为了解各年龄层的人使用手机支付的情况,随机调查50次商业行为,并把调查结果制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
手机支付 | 4 | 6 | 10 | 6 | 2 | 0 |
(1)若从年龄在 [55,65)的被调查者中随机选取2人进行调查,记选中的2人中使用手机支付的人数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)把年龄在[15,45)称为中青年,年龄在[45,75)称为中老年,请根据上表完2×2列联表,是否有![]() 以上的把握判断使用手机支付与年龄(中青年、中老年)有关联?
以上的把握判断使用手机支付与年龄(中青年、中老年)有关联?
手机支付 | 未使用手机支付 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
可能用到的公式: 
独立性检验临界值表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用五种不同颜色(颜色可以不全用完)给三棱柱![]() 的六个顶点涂色,要求每个点涂一种颜色,且每条棱的两个端点涂不同颜色,则不同的涂色种数有( )
的六个顶点涂色,要求每个点涂一种颜色,且每条棱的两个端点涂不同颜色,则不同的涂色种数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市交通管理部门为了解市民对机动车“单双号限行”的态度,随机采访了100名市民,将他们的意见和是否拥有私家车的情况进行了统计,得到了如下的![]() 列联表:
列联表:
赞同限行 | 不赞同限行 | 合计 | |
没有私家车 | 15 | ||
有私家车 | 45 | ||
合计 | 100 |
已知在被采访的100人中随机抽取1人且抽到“赞同限行”者的概率是![]() .
.
(1)请将上面的列联表补充完整;
(2)根据上面的列联表判断能否在犯错误的概率不超过0.10的前提下认为“对限行的态度与是否拥有私家车有关”;
(3)将上述调查所得到的频率视为概率.现在从该市大量市民中,采用随机抽样方法每次抽取1名市民,抽取3次,记被抽取的3名市民中的“赞同限行”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
附:参考公式:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定,疫苗在上市前必须经过严格的检测,并通过临床实验获得相关数据,以保证疫苗使用的安全和有效.某生物制品硏究所将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 40 | p | x |
注射疫苗 | 60 | q | y |
总计 | 100 | 100 | 200 |
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .
.
(1)求![]() 列联表中的数据p,q,
列联表中的数据p,q,![]() ,
,![]() 的值;
的值;
(2)能否有![]() 把握认为注射此种疫苗有效?
把握认为注射此种疫苗有效?
(3)在感染病毒的小白鼠中,按未注射疫苗和注射疫苗的比例抽取5只进行病例分析,然后从这五只小白鼠中随机抽取3只对注射疫苗情况进行核实,求至少抽到2只为未注射疫苗的小白鼠的概率. 附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,且
,且![]() 存在单调递减区间,求实数
存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() ,
, ![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的垂线分别交
轴的垂线分别交![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,证明:
,证明: ![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线不平行.
处的切线不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某食品厂生产的面包中抽取![]() 个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)在相应位置上作出这些数据的频率分布直方图;
(2)估计这种面包质量指标值的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该食品厂生产的这种面包符合“质量指标值不低于![]() 的面包至少要占全部面包
的面包至少要占全部面包![]() 的规定?”
的规定?”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com