
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:不详 题型:单选题
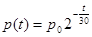 ,其中
,其中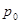 为t=0时的污染物数量,又测得当t=30时,污染物数量的变化率是
为t=0时的污染物数量,又测得当t=30时,污染物数量的变化率是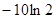 ,则p(60)=
,则p(60)=| A.150毫克/升 | B.300毫克/升 |
| C.150ln2 毫克/升 | D.300ln2毫克/升 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
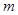 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,建一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,建一个桥墩的工程费用为256万元,距离为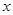 米的相邻两桥墩之间的桥面工程费用为
米的相邻两桥墩之间的桥面工程费用为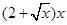 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为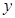 万元。
万元。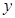 关于
关于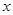 的函数关系式;
的函数关系式; 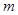 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使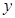 最小?
最小?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
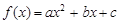 满足:①
满足:①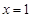 时有极值;②图象过点
时有极值;②图象过点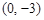 ,且在该点处的切线斜率为
,且在该点处的切线斜率为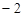 .
.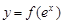 上任意一点的切线的斜率恒大于
上任意一点的切线的斜率恒大于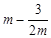 ,求
,求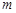 的取值范围;
的取值范围;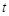 满足什么条件时,函数
满足什么条件时,函数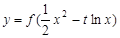 的图象与坐标轴没有公共点?
的图象与坐标轴没有公共点?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com