
Ζ÷Έω Θ®1Θ©…η÷–ΙζΤΙ≈“«ρΡ–Ε”Μώ0ΟΕΫπ≈ΤΘ§≈°Ε”Μώ1ΟΕΫπ≈ΤΈΣ ¬ΦΰAΘ§÷–ΙζΤΙ≈“«ρΡ–Ε”Μώ1ΟΕΫπ≈ΤΘ§≈°Ε”Μώ2ΟΕΫπ≈ΤΈΣ ¬ΦΰBΘ§Α¥¥ΥΙάΦΤ÷–ΙζΤΙ≈“«ρ≈°Ε”±»÷–ΙζΤΙ≈“«ρΡ–Ε”ΕύΜώΒΟ“ΜΟΕΫπ≈ΤΒΡΗ≈¬ PΘ®A+BΘ©=PΘ®AΘ©+PΘ®BΘ©Θ§”…¥ΥΡή«σ≥ωΫαΙϊΘ°
Θ®2Θ©ΗυΨίΧβ“β÷–ΙζΤΙ≈“«ρΕ”ΜώΒΟΫπ≈Τ ΐ «“ΜΥφΜζ±δΝΩΠΈΘ§ΥϋΒΡΥυ”–Ω…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§3Θ§4Θ§Ζ÷±π«σ≥ωœύ”ΠΒΡΗ≈¬ Θ§”…¥ΥΡή«σ≥ωΠΈΒΡΗ≈¬ Ζ÷≤ΦΝ–ΚΆΥυΜώΫπ≈ΤΒΡ ΐ―ßΤΎΆϊΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©…η÷–ΙζΤΙ≈“«ρΡ–Ε”Μώ0ΟΕΫπ≈ΤΘ§≈°Ε”Μώ1ΟΕΫπ≈ΤΈΣ ¬ΦΰAΘ§
÷–ΙζΤΙ≈“«ρΡ–Ε”Μώ1ΟΕΫπ≈ΤΘ§≈°Ε”Μώ2ΟΕΫπ≈ΤΈΣ ¬ΦΰBΘ§
‘ρPΘ®A+BΘ©=PΘ®AΘ©+PΘ®BΘ©
=$C_2^1{Θ®{1-\frac{3}{4}}Θ©^2}•Θ®{\frac{4}{5}}Θ©•Θ®{1-\frac{4}{5}}Θ©$$+C_2^1Θ®{\frac{3}{4}}Θ©•Θ®{1-\frac{3}{4}}Θ©{Θ®{\frac{4}{5}}Θ©^2}=\frac{13}{50}$Θ°
Θ®2Θ©ΗυΨίΧβ“β÷–ΙζΤΙ≈“«ρΕ”ΜώΒΟΫπ≈Τ ΐ «“ΜΥφΜζ±δΝΩΠΈΘ§
ΥϋΒΡΥυ”–Ω…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§3Θ§4Θ®ΒΞΈΜΘΚΟΕΘ©Θ§
Ρ«Ο¥$PΘ®{ΠΈ=0}Θ©=C_2^1{Θ®{1-\frac{3}{4}}Θ©^2}$${Θ®{1-\frac{4}{5}}Θ©^2}=\frac{1}{400}$Θ§
$PΘ®{ΠΈ=1}Θ©=C_2^1Θ®{1-\frac{3}{4}}Θ©•$$Θ®{\frac{3}{4}}Θ©•{Θ®{1-\frac{4}{5}}Θ©^2}+C_2^1Θ®{\frac{4}{5}}Θ©•$${Θ®{1-\frac{3}{4}}Θ©^2}Θ®{1-\frac{4}{5}}Θ©=\frac{7}{200}$Θ§
$PΘ®{ΠΈ=2}Θ©=C_2^1C_2^1Θ®{1-\frac{3}{4}}Θ©•$$Θ®{\frac{3}{4}}Θ©•Θ®{1-\frac{4}{5}}Θ©Θ®{\frac{4}{5}}Θ©+$${Θ®{\frac{4}{5}}Θ©^2}•{Θ®{1-\frac{3}{4}}Θ©^2}{Θ®{1-\frac{4}{5}}Θ©^2}$$Θ®{\frac{3}{4}}Θ©=\frac{73}{400}$Θ§
$PΘ®{ΠΈ=3}Θ©=C_2^1Θ®{1-\frac{3}{4}}Θ©•Θ®{\frac{3}{4}}Θ©$$•{Θ®{\frac{4}{5}}Θ©^2}+C_2^1{Θ®{\frac{3}{4}}Θ©^2}•Θ®{\frac{4}{5}}Θ©$$Θ®{1-\frac{4}{5}}Θ©=\frac{21}{50}$Θ§
$PΘ®{ΠΈ=4}Θ©={Θ®{\frac{3}{4}}Θ©^2}•$${Θ®{\frac{4}{5}}Θ©^2}=\frac{9}{25}$Θ§
‘ρΠΈΒΡΗ≈¬ Ζ÷≤ΦΝ–ΈΣΘΚ
| ΠΈ | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{400}$ | $\frac{7}{200}$ | $\frac{73}{400}$ | $\frac{21}{50}$ | $\frac{9}{25}$ |
ΒψΤά ±ΨΧβΩΦ≤ιΩΦ≤ιΗ≈¬ ΒΡ«σΖ®Θ§ΩΦ≤ιάκ…Δ–ΆΥφΜζ±δΝΩΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊΒΡ«σΖ®Θ§ΩΦ≤ι ΐΨί¥ΠάμΡήΝΠΓΔ‘ΥΥψ«σΫβΡήΝΠΘ§ΩΦ≤ιΜ·Ιι”κΉΣΜ·ΥΦœκΓΔΚ· ΐ”κΖΫΥΦœκΘ§ «÷–ΒΒΧβΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ2016-2017―ßΡξΚ”±± ΓΗΏΕΰάμ…œΒΎ“Μ¥Έ‘¬ΩΦ ΐ―ß ‘ΨμΘ®ΫβΈωΑφΘ© Χβ–ΆΘΚ―Γ‘ώΧβ
»γΆΦ «2015ΡξΡ≥¥σ―ßΉ‘÷ς’–…ζΟφ ‘ΜΖΫΎ÷–Θ§ΤΏΈΜΤάΈ·ΈΣΡ≥ΩΦ…ζ¥ρ≥ωΒΡΖ÷ ΐΒΡΨΞ“ΕΆΦΘ§»ΞΒτ“ΜΗωΉνΗΏΖ÷ΚΆ“ΜΗωΉνΒΆΖ÷ΚσΘ§Υυ Θ ΐΨίΒΡΤΫΨυ ΐΚΆ÷Ύ ΐ“ά¥ΈΈΣΘ® Θ©

AΘ°85Θ§84 BΘ°84Θ§85
CΘ°86Θ§84 DΘ°84Θ§86
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | Θ®-1Θ§0Θ© | BΘ° | Θ®-2Θ§-1Θ© | CΘ° | Θ®-ΓόΘ§0Θ© | DΘ° | Θ®1Θ§+ΓόΘ© |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | Θ®-ΓόΘ§0] | BΘ° | Θ®-ΓόΘ§0]Γ»{$\frac{2}{e}$} | CΘ° | Θ®-ΓόΘ§$\frac{2}{e}$Θ© | DΘ° | Θ®-ΓόΘ§$\frac{2}{e}$Θ© |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
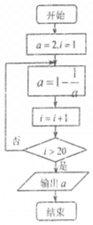
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ΒΎ“Μœσœό | BΘ° | ΒΎΕΰœσœό | CΘ° | ΒΎ»ΐœσœό | DΘ° | ΒΎΥΡœσœό |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $[{\frac{{2\sqrt{5}}}{5}Θ§2}]Γ»[{\frac{{6\sqrt{5}}}{5}Θ§6}]$ | BΘ° | $[{\frac{{2\sqrt{5}}}{5}Θ§6}]$ | CΘ° | $[{\frac{{2\sqrt{5}}}{5}Θ§2}]Γ»[{4Θ§6}]$ | DΘ° | $\left\{2\right\}Γ»[{\frac{{6\sqrt{5}}}{5}Θ§6}]$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com