
分析 (1)由曲线C的参数方程先求出曲线C的普通方程,由此能求出曲线C的极坐标方程.
(2)先求出直线l的直角坐标方程,设p($\sqrt{2}cosα$,sinα),求出点P到直线l的距离,由此利用三角函数能求出|PQ|的最小值.
解答 解:(1)∵曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{2}cosα}\\{y=sinα}\end{array}\right.$,(α为参数),
∴曲线C的普通方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1,
∴曲线C的极坐标方程为ρ2(1+sin2θ)=2.
(2)∵直线l的极坐标方程为$ρcosθ-\sqrt{2}ρsinθ+3=0$.
∴直线l的直角坐标方程为x-$\sqrt{2}y$+3=0.
∵P为曲线C:$\left\{\begin{array}{l}{x=\sqrt{2}cosα}\\{y=sinα}\end{array}\right.$上一点,∴设p($\sqrt{2}cosα$,sinα),
点P到直线l的距离:d=$\frac{|\sqrt{2}cosα-\sqrt{2}sinα+3|}{\sqrt{1+2}}$=$\frac{|2sin(α+\frac{3π}{4})+3|}{\sqrt{3}}$,
∵P为曲线C上一点,Q为直线l上一点,
∴当sin($α+\frac{3π}{4}$)=-1时,|PQ|取最小值dmin=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
点评 本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
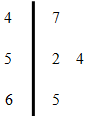 已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.
已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com