
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
分析 运用点满足抛物线的方程可得p(由m表示),运用抛物线的定义可得|AF|,即圆的半径,运用圆的弦长公式,解方程可得m的值.
解答 解:由$A(m,\;\;2\sqrt{2})$在抛物线y2=2px上,
∴2pm=8,∴$p=\frac{4}{m}$,
∴抛物线的焦点$F({\frac{p}{2},\;\;0})$,即$F({\frac{2}{m},\;\;0})$,准线方程为x=-$\frac{p}{2}$,
由抛物线的定义可知$|AF|=m+\frac{p}{2}=m+\frac{2}{m}$,
即圆A的半径$r=m+\frac{2}{m}$.
∵A到y轴的距离d=m,
∴${r^2}-{d^2}={(\sqrt{7})^2}$,
即${({m+\frac{2}{m}})^2}-{m^2}=7$,解得$m=\frac{{2\sqrt{3}}}{3}$,
故选D.
点评 本题考查抛物线的定义和方程的运用,直线和圆相交的弦长公式的运用,考查化简整理的运算能力,属于中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{6}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
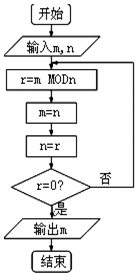 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )| A. | 0 | B. | 5 | C. | 25 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<y<z | B. | y<z<x | C. | z<x<y | D. | z<y<x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com