
分析 (1)函数f(x)=lnx-ax2(a∈R)的零点个数?方程lnx-ax2=0的解(正实数)的个数
?$a=\frac{lnx}{{x}^{2}}$的解的个数?函数y=a,G(x)=$\frac{lnx}{{x}^{2}}$的图象交点个数.利用导数求出单调性,画出草图即可求解.
(2)h(x)=(1-a)x2-kx-f(x)=x2-kx-lnx,h′(x)=2x-$\frac{1}{x}-k$在(0,+∞)单调递增,
不妨设m>n>0,则$\sqrt{mn}$<c<$\frac{m+n}{2}$?$h′(\sqrt{mn})<h′(c)=\frac{h(m)-h(n)}{m-n}<$h′($\frac{m+n}{2}$).
?m+n-$\frac{lnm-lnn}{m-n}$-k<m+n-$\frac{2}{m+n}-k$…①,2$\sqrt{mn}$-$\frac{1}{\sqrt{mn}}$-k<m+n-$\frac{lnm-lnn}{m-n}$-k…②
分别对①②时求证即可.
解答 解:(1),函数f(x)的定义域为(0,+∞),
函数f(x)=lnx-ax2(a∈R)的零点个数?方程lnx-ax2=0的解(正实数)的个数
?$a=\frac{lnx}{{x}^{2}}$的解的个数?函数y=a,G(x)=$\frac{lnx}{{x}^{2}}$的图象交点个数.
G′(x)=$\frac{1-2lnx}{{x}^{3}}$,令G′(x)=0得x=$\sqrt{e}$
x$∈(0,\sqrt{e})$时,G′(x)>0,x$∈(\sqrt{e}$,+∞)时,G′(x)<0,∴函数G(x)在(0,$\sqrt{e}$)递增,在($\sqrt{e},+∞$)递减,
且x>1时.G(x)>0,x<1时,G(x)<0,G(x)max=G($\sqrt{e}$)=$\frac{1}{2e}$,
其草图如下:由图象可知:
$a>\frac{1}{2e}$时,函数f(x)无零点,0<a<$\frac{1}{2e}$时,又两个零点,a=$\frac{1}{2e}$时,有有一个零点.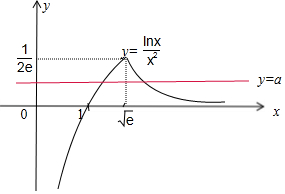
证明:(2)h(x)=(1-a)x2-kx-f(x)=x2-kx-lnx,h′(x)=2x-$\frac{1}{x}-k$在(0,+∞)单调递增,
不妨设m>n>0,则$\sqrt{mn}$<c<$\frac{m+n}{2}$?$h′(\sqrt{mn})<h′(c)=\frac{h(m)-h(n)}{m-n}<$h′($\frac{m+n}{2}$).
?m+n-$\frac{lnm-lnn}{m-n}$-k<m+n-$\frac{2}{m+n}-k$…①,2$\sqrt{mn}$-$\frac{1}{\sqrt{mn}}$-k<m+n-$\frac{lnm-lnn}{m-n}$-k…②
由①得$\frac{lnm-lnn}{m-n}>\frac{2}{m+n}$?$ln\frac{m}{n}>\frac{2(m-n)}{m+n}=\frac{\frac{m}{n}-1}{\frac{m}{n}+1}$,
令t=$\frac{m}{n}$>1,可构造函数g(t)=lnt-$\frac{2(t-1)}{t+1}$,(t>1),g′(t)=$\frac{(t-1)^{2}}{t(t+1)}>$0,则g(t)在(1,+∞)单调递增,即g(t)>g(1)=0,故①成立.
在②中∵$m+n>2\sqrt{mn}$成立,只需证明$\frac{1}{\sqrt{mn}}>\frac{lnm-lnn}{m-n}$?ln$\frac{m}{n}$<$\frac{m-n}{\sqrt{mn}}$=$\sqrt{\frac{m}{n}}-\sqrt{\frac{n}{m}}$,
令$\sqrt{\frac{m}{n}}=t$>1,可构造函数φ(t)=2lnt-(t-$\frac{1}{t}$)(t>1),φ′(t)=-$\frac{(t-1)^{2}}{{t}^{2}}$<0,函数φ(t)在(1,+∞)单调递减,即φ(t)<φ(1)=0,故②成立.
综上,原结论成立
点评 该题考查利用导数研究函数的单调性、极值和函数的零点,考查学生综合运用知识分析解决问题的能力,该题运算量大,综合性强,能力要求高,属于压轴题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
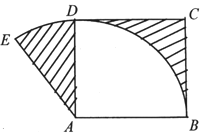 如图,以正方形ABCD中的点A为圆心,边长AB为半径作扇形EAB,若图中两块阴影部分的面积相等,则∠EAD的弧度数大小为2-$\frac{π}{2}$.
如图,以正方形ABCD中的点A为圆心,边长AB为半径作扇形EAB,若图中两块阴影部分的面积相等,则∠EAD的弧度数大小为2-$\frac{π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com