
分析 (Ⅰ)求出函数的导数,解关于导函数的方程,求出函数的单调区间,求出函数的最大值,通过讨论a的范围,判断函数的零点个数即可;
(Ⅱ)通过讨论a的范围,求出函数f(x)的值域,通过讨论t的范围,求出g(x)的最值,结合集合的包含关系证明结论即可.
解答 解:(Ⅰ)f(x)的定义域是(0,+∞),f′(x)=$\frac{a{-x}^{2}}{x}$,
令f′(x)=0,解得:x=$\sqrt{a}$或x=-$\sqrt{a}$(舍),
x∈(0,$\sqrt{a}$)时,f′(x)>0,f(x)递增,
x∈($\sqrt{a}$,+∞)时,f′(x)<0,f(x)递减,
故f(x)max=f($\sqrt{a}$)=$\frac{1}{2}$a(lna-1),
令h(a)=$\frac{1}{2}$a(lna-1),a∈[1,e2],则h′(a)=$\frac{1}{2}$lna≥0,
故函数h(a)在[1,e2]递增,
故h(1)≤h(a)≤h(e2),即-$\frac{1}{2}$≤h(a)≤$\frac{1}{2}$e2,
令h(a)=0,则a=e,
a∈[1,e)时,h(a)<0,即f(x)max<0,此时f(x)无零点,
a=e时,h(a)=0,即f(x)max=0,f(x)有1个零点,
a∈(e,e2]时,h(a)>0,即f(x)max>0,
由函数f(x)的定义域可知x→0时,lnx→-∞,
$\frac{1}{2}$x2→0,故f(x)→-∞,x→+∞时,f(x)→-∞,
故此时f(x)有2个零点,
综上,a∈[1,e)时,函数f(x)无零点,a=e时,函数f(x)有唯一零点,
a∈(e,e2]时,函数f(x)有2个零点;
(Ⅱ)由(Ⅰ)得:a∈[1,e]时,f(x)max=f($\sqrt{a}$)≤0,又f(1)=-$\frac{1}{2}$,
f($\sqrt{e}$)=$\frac{1}{2}$(a-e)∈[$\frac{1}{2}$(1-e),0],
当$\frac{1}{2}$(a-e)≥-$\frac{1}{2}$时,函数f(x)=alnx-$\frac{1}{2}$x2,(x∈[1,$\sqrt{e}$)的值域是:
[-$\frac{1}{2}$,$\frac{1}{2}$a(lna-1)]⊆[-$\frac{1}{2}$,0],
当$\frac{1}{2}$(a-e)<-$\frac{1}{2}$时,函数f(x)=alnx-$\frac{1}{2}$x2(x∈[1,$\sqrt{e}$]的值域是:
[$\frac{1}{2}$(a-e),$\frac{1}{2}$a(lna-1)]⊆[$\frac{1}{2}$(1-e),$\frac{1}{2}$a(lna-1)]?[-1,0],
由上可知,对于任意的x1∈[1,$\sqrt{e}$],f(x1)∈[-1,0],
对于函数g(x),g(x)=tx2-4x+1=t${(x-\frac{2}{t})}^{2}$+1-$\frac{4}{t}$,x∈[0,1],
当-2≤t<0时,$\frac{2}{t}$<0,g(x)在区间[0,1]递减,
当t=0时,g(x)=-4x+1,g(x)在区间[0,1]递减,
0<t≤2时,$\frac{2}{t}$≥1,g(x)在区间[0,1]递减,
故t∈[-2,2]时,g(x)min=g(1)=t-3∈[-5,-1],g(x)max=g(0)=1,
故x2∈[0,1]时,g(x2)∈[-1,0]?[t-3,1],
故对任意的${x_1}∈[1,\sqrt{e}]$,存在x2∈[0,1],使得f(x1)=g(x2).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,考查函数的零点问题,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
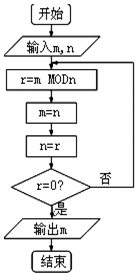 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )| A. | 0 | B. | 5 | C. | 25 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,5) | B. | [3,5] | C. | (2,4) | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<y<z | B. | y<z<x | C. | z<x<y | D. | z<y<x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com