
分析 利用导函数求解出切线方程,设出切点为(θ,-sinθ),π<θ<$\frac{3π}{2}$,求出f(x)=sinx的导函数,斜率k相等,可得θ的值.即可求解.
解答 解:函数f(x)=|sinx|(x≥0)的图象与过原点的直线恰有三个交点,
设出切点为(θ,-sinθ),π<θ<$\frac{3π}{2}$,
则f(x)=sinx的导函数f′(x)=-cosx,
∴f′(θ)=-cosθ=$-\frac{sinθ}{θ}$,
可得:θ=tanθ,
sin2θ=2sinθcosθ.
则$\frac{{(1+{θ^2})sin2θ}}{θ}$=$\frac{(1+ta{n}^{2}θ)sin2θ}{tanθ}$=$\frac{sin2θ+\frac{sinθ•sinθ}{cosθ•cosθ}×2sinθcosθ}{\frac{sinθ}{cosθ}}$=2sin2θ+2cos2θ=2.
故答案为2.
点评 本题考查了导函数的几何意义的运用.属于中档题.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
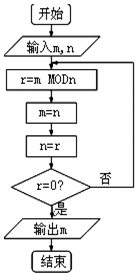 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )| A. | 0 | B. | 5 | C. | 25 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,5) | B. | [3,5] | C. | (2,4) | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶人数 | 45 | 10 | 55 |
| 女性驾驶人数 | 25 | 20 | 45 |
| 合计 | 70 | 30 | 100 |
| P(k2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<y<z | B. | y<z<x | C. | z<x<y | D. | z<y<x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com