
| A. | (-1,0) | B. | (-2,-1) | C. | (-∞,0) | D. | (1,+∞) |
分析 利用导数法,分析函数的单调性及极值,可得f(x1)=f(x2)=f(x3)∈(0,$\frac{1}{e}$),进而可得:-$\frac{2}{e}$<x1<-$\frac{1}{e}$,故$\frac{{f({x_2})}}{x_1}$=$\frac{f({x}_{1})}{{x}_{1}}$=1+$\frac{\frac{2}{e}}{{x}_{1}}$∈(-1,0).
解答 解:函数f(x)=$\left\{\begin{array}{l}x+\frac{2}{e},x<0\\ \frac{x}{e^x},x≥0\end{array}$,
∴函数f′(x)=$\left\{\begin{array}{l}1,x<0\\ \frac{1-x}{{e}^{x}},x≥0\end{array}\right.$,
故当x<0时,函数为增函数,且f(x)<$\frac{2}{e}$,
当0≤x<1时,函数为增函数,且0≤f(x)<$\frac{1}{e}$,
当x≥1时,函数为减函数,且0<f(x)≤$\frac{1}{e}$,
若f(x1)=f(x2)=f(x3)(x1<x2<x3),
则f(x1)=f(x2)=f(x3)∈(0,$\frac{1}{e}$),
即-$\frac{2}{e}$<x1<-$\frac{1}{e}$,
故$\frac{{f({x_2})}}{x_1}$=$\frac{f({x}_{1})}{{x}_{1}}$=1+$\frac{\frac{2}{e}}{{x}_{1}}$∈(-1,0),
故选:A
点评 本题考查的知识点是分段函数的应用,利用导数法研究函数的单调性,利用导数法研究函数的极值,难度中档.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:解答题
直线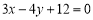 与坐标轴的交点是圆
与坐标轴的交点是圆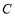 一条直径的两端点.
一条直径的两端点.
(I)求圆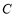 的方程;
的方程;
(II)圆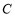 的弦
的弦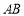 长度为
长度为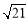 且过点
且过点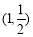 ,求弦
,求弦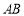 所在直线的方程.
所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{15}$ | B. | $\frac{2}{15}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com