
分析 由定积分的几何意义可求a值,再由二项式定理可得.
解答 解:a=${∫}_{-2}^{2}$$\sqrt{4-{x}^{2}}$dx表示圆x2+y2=4面积的一半,
故a=$\frac{1}{2}$×π×22=2π,∴(ax+$\frac{1}{x}$)6=(2πx+$\frac{1}{x}$)6,
展开式通项为Tk+1=${C}_{6}^{k}$(2πx)6-k($\frac{1}{x}$)k=${C}_{6}^{k}$(2π)6-kx6-2k,
令6-2k=0可解得k=3,故展开式中的常数项为T4=${C}_{6}^{3}$(2π)3=160π3,
故答案为:160π3.
点评 本题考查几何意义求定积分和二项式定理,属中档题.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | [1,3] | C. | [-1,11] | D. | [-5,11] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 3或5 | D. | 4或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
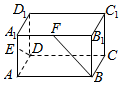 如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )
如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com