
已知函数f(x)=
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a=1,函数 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值.
(1)当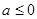 时,
时,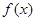 在
在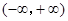 上为增函数;当
上为增函数;当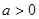 时,
时,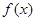 在
在 为减函数,在
为减函数,在 为增函数;(2)
为增函数;(2)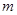 的最大值为1.
的最大值为1.
解析试题分析:(1)讨论函数的单调性首先注意明确函数的定义域,由于该函数是超越函数与一次函数的和构成的,所以考虑用导数,先求出函数的导数得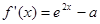 ,由指数函数的性质可知要确定导数的正负须按
,由指数函数的性质可知要确定导数的正负须按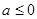 和
和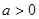 分类讨论,确定导数的符号而求出函数的单调区间;(2)函数
分类讨论,确定导数的符号而求出函数的单调区间;(2)函数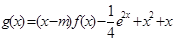 在区间(0,+
在区间(0,+ )上为增函数
)上为增函数 在
在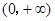 恒成立,分离参数m,从而将所求问题转化为求函数的最值问题,构造新函数,再用导数研究此函数的最小值即可;注意所求的m为整数这一特性.
恒成立,分离参数m,从而将所求问题转化为求函数的最值问题,构造新函数,再用导数研究此函数的最小值即可;注意所求的m为整数这一特性.
试题解析:(1)定义域为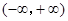 ,
,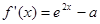 ,
,
当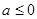 时,
时,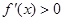 ,所以
,所以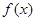 在
在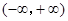 上为增函数; 2分
上为增函数; 2分
当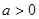 时,由
时,由 得
得 ,且当
,且当 时,
时, ,
,
当 时
时 ,
,
所以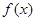 在
在 为减函数,在
为减函数,在 为增函数. 6分
为增函数. 6分
(2)当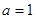 时,
时,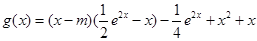 ,
,
若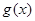 在区间
在区间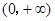 上为增函数,
上为增函数,
则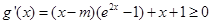 在
在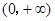 恒成立,
恒成立,
即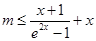 在
在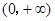 恒成立 8分
恒成立 8分
令 ,
,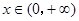 ;
; ,
,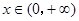 ;令
;令 ,
,
可知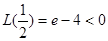 ,
,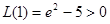 ,
,
又当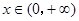 时
时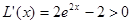 ,
,
所以函数 在
在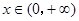 只有一个零点,设为
只有一个零点,设为 ,即
,即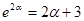 ,
,
且 ; 9分
; 9分
由上可知当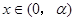 时
时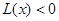 ,即
,即 ;当
;当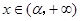 时
时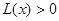 ,即
,即 ,
,
所以 ,
,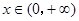 ,有最小值
,有最小值 , 10分
, 10分
把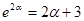 代入上式可得
代入上式可得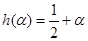 ,又因为
,又因为 ,所以
,所以 ,
,
又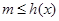 恒成立,所以
恒成立,所以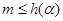 ,又因为
,又因为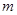 为整数,
为整数,
所以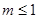 ,所以整数
,所以整数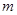 的最大值为1. 12分
的最大值为1. 12分
考点:1.利用函数的导数求单调区间;2.利用函数的导数求最值;3.不等式的恒成立.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
已知关于 的函数
的函数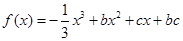 ,其导函数为
,其导函数为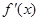 .记函数
.记函数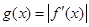 在区间
在区间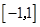 上的最大值为
上的最大值为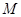 .
.
(1) 如果函数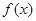 在
在 处有极值
处有极值 ,试确定
,试确定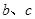 的值;
的值;
(2) 若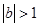 ,证明对任意的
,证明对任意的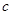 ,都有
,都有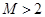 ;
;
(3) 若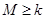 对任意的
对任意的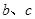 恒成立,试求
恒成立,试求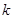 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于三次函数
 。
。
定义:(1)设 是函数
是函数 的导数
的导数 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”;
的“拐点”;
定义:(2)设 为常数,若定义在
为常数,若定义在 上的函数
上的函数 对于定义域内的一切实数
对于定义域内的一切实数 ,都有
,都有 成立,则函数
成立,则函数 的图象关于点
的图象关于点 对称。
对称。
己知 ,请回答下列问题:
,请回答下列问题:
(1)求函数 的“拐点”
的“拐点” 的坐标
的坐标
(2)检验函数 的图象是否关于“拐点”
的图象是否关于“拐点” 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数 ,使得它的“拐点”是
,使得它的“拐点”是 (不要过程)
(不要过程)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,抛物线 与
与 轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在
轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在 轴上.已知工业用地每单位面积价值为
轴上.已知工业用地每单位面积价值为 元
元 ,其它的三个边角地块每单位面积价值
,其它的三个边角地块每单位面积价值 元.
元.
(1)求等待开垦土地的面积;
(2)如何确定点C的位置,才能使得整块土地总价值最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com