
已知二次函数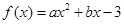 在
在 处取得极值,且在
处取得极值,且在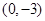 点处的切线与直线
点处的切线与直线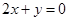 平行.
平行.
(1)求 的解析式;
的解析式;
(2)求函数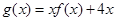 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数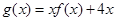 在
在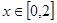 的最值。
的最值。
(1)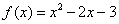 (2)函数g(x)的单调递增区间为(﹣∞,
(2)函数g(x)的单调递增区间为(﹣∞, ),(1,+∞).在x2=1有极小值为0.在
),(1,+∞).在x2=1有极小值为0.在 有极大值
有极大值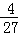 .(3)函数g(x)的最大值为2,最小值为0.
.(3)函数g(x)的最大值为2,最小值为0.
解析试题分析:(1)由f(x)=ax2+bx﹣3,知f′(x)=2ax+b.由二次函数f(x)=ax2+bx﹣3在x=1处取得极值,且在(0,﹣3)点处的切线与直线2x+y=0平行,知
科目:高中数学
来源:
题型:解答题
某商场预计从2013年1月份起的前x个月,顾客对某商品的需求总量p(x)(单位:件)与x的关系近似的满足
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
已知函数f(x)=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 ,由此能求出f(x).
,由此能求出f(x).
(2)由f(x)=x2﹣2x﹣3,知g(x)=xf(x)+4x=x3﹣2x2+x,所以g′(x)=3x2﹣4x+1=(3x﹣1)(x﹣1).令g′(x)=0,得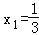 ,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
(3)由g(0)=0,g(2)=2,结合(2)的结论,能求出函数g(x)的最大值和最小值.
试题解析:(1)由 ,可得
,可得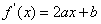 . 由题设可得
. 由题设可得 即
即
解得 ,
,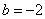 .所以
.所以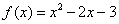 .
.
(2)由题意得 ,所以
,所以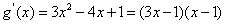 .令
.令 ,得
,得 ,
,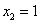 .
. 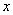
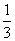
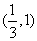
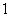
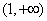
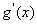
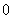

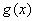
4/27 

口算题卡西安出版社系列答案
黄冈360度口算应用题卡系列答案
希望考苑能力测评卷系列答案
名师金卷系列答案
课堂作业武汉出版社系列答案

全优读本系列答案
同步练习四川教育出版社系列答案
长江全能学案实验报告系列答案
读写双优阅读与写作专项训练系列答案
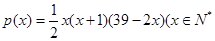 ,且
,且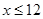 )。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
)。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
(1)写出这种商品2013年第x月的需求量f(x)(单位:件)与x的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问该商场2013年第几个月销售该商品的月利润最大,最大月利润为多少元?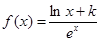 (k为常数,e=2.71828…是自然对数的底数),曲线
(k为常数,e=2.71828…是自然对数的底数),曲线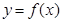 在点
在点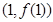 处的切线与x轴平行.
处的切线与x轴平行.
(1)求k的值及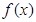 的单调区间;
的单调区间;
(2)设 其中
其中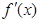 为
为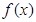 的导函数,证明:对任意
的导函数,证明:对任意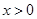 ,
,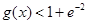 .
.
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a=1,函数 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号