
设函数f(x)=ax-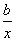 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
解析 (1)方程7x-4y-12=0可化为y=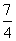 x-3,
x-3,
当x=2时,y=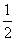 .又f′(x)=a+
.又f′(x)=a+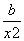 ,于是
,于是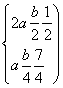
解得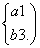 故f(x)=x-
故f(x)=x-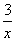 .
.
(2)证明 设P(x0,y0)为曲线上任一点,
由f′(x)=1+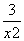 知,曲线在点P(x0,y0)处的切线方程为y-y0=
知,曲线在点P(x0,y0)处的切线方程为y-y0=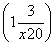 (x-x0),
(x-x0),
即y-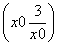 =
=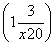 (x-x0).
(x-x0).
令x=0得,y=-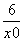 ,从而得切线与直线x=0交点坐标为
,从而得切线与直线x=0交点坐标为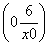 .
.
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0).
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为
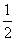
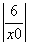 |2x0|=6.
|2x0|=6.
故曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,此定值为6.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为( ).
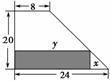
A.x=15,y=12 B.x=12,y=15
C.x=14,y=10 D.x=10,y=14
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线为l:
3x-y+1=0,若x=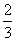 时,y=f(x)有极值.
时,y=f(x)有极值.
(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com