
图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题
(1) 求证:MN//平面PBD; (2)求证:AQ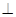 平面PBD;
平面PBD;
(3)求二面角P-DB-M的余弦值。
(1)只需证MN//BD;(2)只需证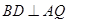 ,
, 。(3)
。(3) 。
。
解析试题分析:画出MN和PB如图所示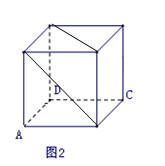
(1) 证明:在正方体ABCD-PMQN中 MN//BD
MN//BD
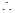 MN//平面PBD
MN//平面PBD
(2)证明:在正方体ABCD-PMQN中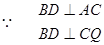

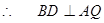
同理可证 : 

(3)解: 建立空间直角坐标系如图所示,设正方体的棱长为1
则 A(1,0,0), Q(0,1,1) , C(0,1,0)
由知平面PBD的一个法向量是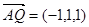
平面MBD的一个法向量是

 二面角P-DB-M的余弦值为
二面角P-DB-M的余弦值为  .
.
考点:正方体的的平面展开图;线面平行的判定定理;线面垂直的判定定理;二面角。
点评:综合法求二面角,往往需要作出平面角,这是几何中一大难点,而用向量法求解二面角无需作出二面角的平面角,只需求出平面的法向量,经过简单运算即可,从而体现了空间向量的巨大作用.二面角的向量求法: ①若AB、CD分别是二面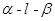 的两个半平面内与棱
的两个半平面内与棱 垂直的异面直线,则二面角的大小就是向量
垂直的异面直线,则二面角的大小就是向量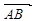 与
与 的夹角; ②设
的夹角; ②设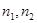 分别是二面角
分别是二面角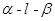 的两个面α,β的法向量,则向量
的两个面α,β的法向量,则向量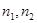 的夹角(或其补角)的大小就是二面角的平面角的大小。
的夹角(或其补角)的大小就是二面角的平面角的大小。


科目:高中数学 来源: 题型:解答题
如图,圆锥 中,
中, 为底面圆的两条直径 ,AB交CD于O,且
为底面圆的两条直径 ,AB交CD于O,且 ,
, ,
, 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求圆锥 的表面积;求圆锥
的表面积;求圆锥 的体积。
的体积。
(3)求异面直线 与
与 所成角的正切值 .
所成角的正切值 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知一个四棱锥的三视图如图所示,其中 ,且
,且 ,
, 分别为
分别为 、
、 、
、 的中点
的中点
(1)求证:PB//平面EFG
(2)求直线PA与平面EFG所成角的大小
(3)在直线CD上是否存在一点Q,使二面角 的大小为
的大小为 ?若存在,求出CQ的长;若不存在,请说明理由。
?若存在,求出CQ的长;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
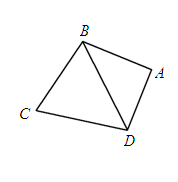
(本小题满分12分)如图4平面四边形ABCD中,AB=AD=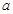 ,BC=CD=BD,设
,BC=CD=BD,设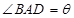 .
.
(1)将四边形ABCD的面积S表示为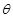 的函数;
的函数;
(2)求四边形ABCD面积S的最大值及此时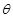 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com