
分析 (1)由题意可得函数h(x)=$\frac{1}{2}$f(x)-x-|2x-a|有四个不同零点,即有y=$\frac{1}{2}$x2与y=|2x-a|有四个不同的交点,分别作出它们的图象,求得它们有三个交点的情况,再由图象平移即可得到a的范围;
(2)不等式可化为c≤2x2-|x-1|,运用二次函数的最值方法,求出右边函数的最小值,即可得到c的范围.
解答 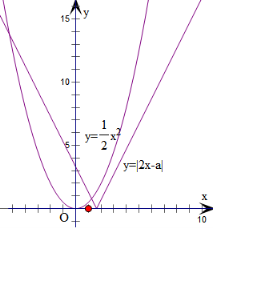 解:(1)h(x)=$\frac{1}{2}$f(x)-x-|2x-a|
解:(1)h(x)=$\frac{1}{2}$f(x)-x-|2x-a|
=$\frac{1}{2}$(x2+2x)-x-|2x-a|=$\frac{1}{2}$x2-|2x-a|,
函数h(x)=$\frac{1}{2}$f(x)-x-|2x-a|有四个不同零点,
即有y=$\frac{1}{2}$x2与y=|2x-a|有四个不同的交点,
由y=$\frac{1}{2}$x2与y=2x-a可得$\frac{1}{2}$x2-2x+a=0,
令判别式△=4-2a=0,解得a=2,此时有三个交点.
由y=$\frac{1}{2}$x2与y=a-2x可得$\frac{1}{2}$x2+2x-a=0,
令判别式△=4+2a=0,解得a=-2,此时有三个交点.
当a=0时,由y=$\frac{1}{2}$x2与y=|2x|,此时有三个交点.
由图象平移观察可得所求a的范围是:(-2,0)∪(0,2);
(2)由函数f(x)和g(x)的图象关于原点对称,
g(x)=-f(-x)=-(x2-2x)=2x-x2,
原不等式可化为c≤2x2-|x-1|,
令F(x)=2x2-|x-1|=$\left\{\begin{array}{l}{2{x}^{2}-x+1,x≥1}\\{2{x}^{2}+x-1,x<1}\end{array}\right.$,
当x≥1时,F(x)=2(x-$\frac{1}{4}$)2+$\frac{7}{8}$递增,最小值为f(1)=2;
当x<1时,F(x)=2(x+$\frac{1}{4}$)2-$\frac{9}{8}$,最小值为F(-$\frac{1}{4}$)=-$\frac{9}{8}$.
即有F(x)min=F(-$\frac{1}{4}$)=-$\frac{9}{8}$,即为c≤-$\frac{9}{8}$.
则c的取值范围是(-∞,-$\frac{9}{8}$].
点评 本题主要考查绝对值函数的图象和性质,注意化为分段函数,同时考查图象平移和不等式恒成立问题转化为求函数的最值问题,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x${\;}^{\frac{1}{2}}$ | B. | f(x)=x3 | C. | f(x)=($\frac{1}{2}$)x | D. | f(x)=3x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
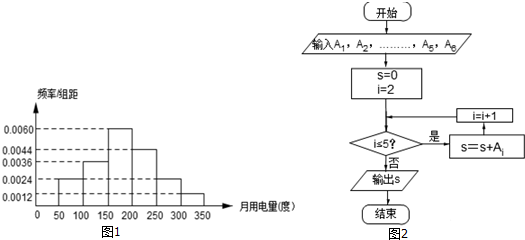
| A. | 820 | B. | 720 | C. | 620 | D. | 520 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com