
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
分析 根据双曲线的定义知a,根据双曲线方程可得它的渐近线方程为bx±ay=0,利用点到直线的距离,结合已知条件列式,可得b,再用平方关系可算出c,最后利用双曲线离心率的公式,可以计算出该双曲线的离心率.
解答 解:根据双曲线的定义知,2a=2$\sqrt{2}$,∴a=$\sqrt{2}$,
双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线的方程为bx-ay=0或bx+ay=0,
点P(x0,y0)到两条渐近线的距离之积为$\frac{|b{x}_{0}-a{y}_{0}|}{\sqrt{{a}^{2}+{b}^{2}}}•\frac{|b{x}_{0}+a{y}_{0}|}{\sqrt{{a}^{2}+{b}^{2}}}=\frac{2}{3}$,
∴$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}=\frac{2}{3}$,即$\frac{2{b}^{2}}{2+{b}^{2}}=\frac{2}{3}$,
∴b=1,∴c=$\sqrt{3}$,
则双曲线的离心率为e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$.
故选:D.
点评 本题给出双曲线一个焦点到渐近线的距离与到左焦点的距离与到右焦点的距离之差,求双曲线的离心率,着重考查了双曲线的标准方程和简单几何性质等知识,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 地区类别 | 首小时内 | 首小时外 |
| 一类 | 2.5元/15分钟 | 3.75元/15分钟 |
| 二类 | 1.5元/15分钟 | 2.25元/15分钟 |
| 三类 | 0.5元/15分钟 | 0.75元/15分钟 |
| A. | 一类 | B. | 二类 | C. | 三类 | D. | 无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
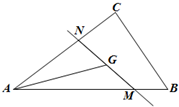 如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )
如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1、0.、0.8 | B. | 0.6、0.8、1 | C. | 0.6、1、0.8 | D. | 0.6、0.6、0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com