练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．江苏舜天足球俱乐部为救助在“3.10云南盈江地震”中失学的儿童，准备在江苏省五台山体育场举行多场足球义赛，预计卖出门票2.4万张，票价分别为3元、5元和8元三种，且票价3元和5元的张数的积为0.6万张．设x是门票的总收入，经预算扣除其它各项开支后，该俱乐部的纯收入函数模型为y=lg2x，则当这三种门票的张数分别为（　　）万张时，可以为失学儿童募捐的纯收入最大．
    A．1、0．、0.8B．0.6、0.8、1C．0.6、1、0.8D．0.6、0.6、0.8

    分析 设3元、5元、8元门票的张数分别为a，b，c，由题意可得$\left\{\begin{array}{l}{a+b+c=2.4}\\{ab=0.6}\\{x=3a+5b+8c}\end{array}\right.$，从而由基本不等式可得x=19.2-（5a+3b）≤19.2-2$\sqrt{15ab}$=13.2；从而可得$\left\{\begin{array}{l}{5a=3b}\\{ab=0.6}\end{array}\right.$，从而解得a=0.6，b=1，c=0.8．

    解答 解：设3元、5元、8元门票的张数分别为a，b，c，
    则有$\left\{\begin{array}{l}{a+b+c=2.4}\\{ab=0.6}\\{x=3a+5b+8c}\end{array}\right.$，
    整理得，
    x=19.2-（5a+3b）≤19.2-2$\sqrt{15ab}$=13.2（万元）．
    当且仅当$\left\{\begin{array}{l}{5a=3b}\\{ab=0.6}\end{array}\right.$时等号成立，
    解得，a=0.6，b=1，
    所以c=0.8．
    由于y=lg2x为增函数，
    即此时y也恰有最大值．
    故三种门票的张数分别为0.6、1、0.8万张时可以为失学儿童募捐的纯收入最大．
    故选C．

    点评 本题考查了基本不等式在实际问题中的应用，同时考查了对数函数及指数函数的性质应用，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）右支上的一点P（x0，y0）到左焦点的距离与到右焦点的距离之差为2$\sqrt{2}$，且到两条渐进线的距离之积为$\frac{2}{3}$，则该双曲线的离心率为（　　）
    A．$\sqrt{5}$B．$\sqrt{6}$C．$\frac{\sqrt{5}}{2}$D．$\frac{\sqrt{6}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．图1为某村1000户村民月用电量（单位：度）的频率分布直方图，记月用电量在[50，100）的用户数为A1，用电量在[100，150）的用户数为A2，…，以此类推，用电量在[300，350]的用户数为A6，图2是统计图1中村民月用电量在一定范围内的用户数的一个算法流程图．根据图1提供的信息，则图2中输出的s值为（　　）
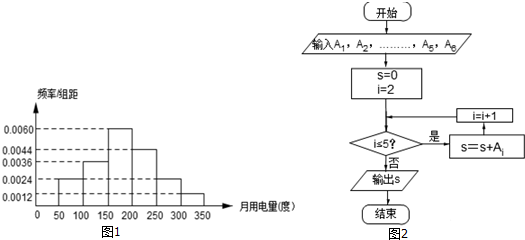
    A．820B．720C．620D．520

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．在直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}{x=1+\sqrt{2}cosα}\\{y=1+\sqrt{2}sinα}\end{array}\right.$（α为参数），以坐标原点O为极点，以x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程是ρcos（θ-$\frac{π}{4}$）=$\sqrt{2}$．
    （1）写出曲线C的普通方程，直线l的直角坐标方程；
    （2）设P为曲线C上任意一点，直线l和曲线C交于A，B两点，求|PA|2+|PB|2+|PO|2的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．正弦曲线y=sinx在点（$\frac{π}{3}$，$\frac{\sqrt{3}}{2}$）的切线方程是（　　）
    A．x+2y-$\sqrt{3}$+$\frac{π}{3}$=0B．x-2y+$\sqrt{3}$-$\frac{π}{3}$=0C．$\sqrt{3}$x-2y+$\sqrt{3}$-$\frac{\sqrt{3}}{3}$π=0D．$\sqrt{3}$x+2y-$\sqrt{3}$+$\frac{\sqrt{3}}{3}$π=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．在平面直角坐标系xOy中，双曲线中心在原点，焦点在y轴上，离心率为$\sqrt{5}$，则其渐进线方程为（　　）
    A．y=$\frac{1}{2}$xB．y=±$\frac{1}{2}$xC．y=-$\frac{1}{2}$xD．y=±2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知过点（1，1）的直线与圆x2+y2-4x-6y+4=0相交于A，B两点，则|AB|的最小值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知i是虚数单位，a为实数，z为纯虚数，1+z=a+$\frac{1+i}{1-i}$，则z=（　　）
    A．1B．-1C．iD．-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知数列{an}的前n项和Sn=2an-2n+1+2（n为正整数）．
    （1）证明：数列{$\frac{{a}_{n}}{{2}^{n}}$}是等差数列，并求{an}的通项公式；
    （2）令bn=log2a1+log2$\frac{{a}_{2}}{2}$+…+log2$\frac{{a}_{n}}{n}$，设数列{$\frac{1}{{b}_{n}}$}的前n项和为Tn，是否存在实数M，使得Tn≤M对一切正整数都成立？若存在，求出M的最小值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案