
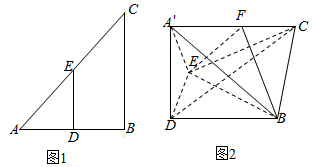
 ��ͼ1��Rt��ABC�У���ABC=90�㣬D��E�ֱ�Ϊ�߶�AB��AC���е㣬AB=4��BC=2$\sqrt{2}$����DEΪ�ۺۣ���Rt��ADE����ͼ2��λ�ã�ʹƽ��A��DE��ƽ��DBCE������A��C����B����F���߶�A��C�ϵĶ��㣬����$\overrightarrow{CF}$=��$\overrightarrow{CA��}$��
��ͼ1��Rt��ABC�У���ABC=90�㣬D��E�ֱ�Ϊ�߶�AB��AC���е㣬AB=4��BC=2$\sqrt{2}$����DEΪ�ۺۣ���Rt��ADE����ͼ2��λ�ã�ʹƽ��A��DE��ƽ��DBCE������A��C����B����F���߶�A��C�ϵĶ��㣬����$\overrightarrow{CF}$=��$\overrightarrow{CA��}$������ ������ƽ��A��DE��ƽ��DBCE��A��D��DE���ɵ�A��D��BE����ֱ��������DEB�У�tan��BED=$\sqrt{2}$��tan��CDE=$\frac{\sqrt{2}}{2}$���ɵá�BED+��CDE=90�㣬�ɵ�BE��DC���ɵ�BE��ƽ��A��DC������֤�����ۣ�
��II����DΪ����ԭ��DB��DE��DA��ֱ�ΪOX��OY��OZ�Ὠ���ռ�ֱ������ϵ����ƽ��BEF�ķ�����Ϊ$\overrightarrow{n}$=��x��y��z��������$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BE}=0}\\{\overrightarrow{n}•\overrightarrow{BF}=0}\end{array}\right.$���ɵó���ȡƽ��BEC�ķ�����Ϊ$\overrightarrow{m}$=��0��0��1�������������нǹ�ʽ���ɵó���
���  �⣺����ƽ��A��DE��ƽ��DBCE��A��D��DE��
�⣺����ƽ��A��DE��ƽ��DBCE��A��D��DE��
��A��D��ƽ��DBCE����A��D��BE��
��D��E�ֱ�Ϊ�е㣬
��DE=$\frac{1}{2}$BC=$\sqrt{2}$��BD=$\frac{1}{2}$AB=2��
��ֱ��������DEB�У�tan��BED=$\frac{BD}{DE}$=$\sqrt{2}$��tan��CDE=$\frac{BD}{CB}$=$\frac{\sqrt{2}}{2}$��
��tan��BED•tan��CDE=1��
���BED+��CDE=90�㣬�ɵ�BE��DC��
��BE��ƽ��A��DC����BE?ƽ��FEB��
��ƽ��FBE��ƽ��A��DC��
��II����DΪ����ԭ��DB��DE��DA��ֱ�ΪOX��OY��OZ�Ὠ���ռ�ֱ������ϵ����������ֱ�ΪD��0��0��0����A�䣨0��0��2����B��2��0��0����
C��2��2$\sqrt{2}$��0����E��0��$\sqrt{2}$��0����$\overrightarrow{C{A}^{��}}$��-2��-2$\sqrt{2}$��2����
��$\overrightarrow{CF}$=��$\overrightarrow{CA��}$����$\overrightarrow{CF}$=�ˣ�-2��-2$\sqrt{2}$��-2������F$��2-2�ˣ�2\sqrt{2}-2\sqrt{2}�ˣ�2�ˣ�$��
��ƽ��BEF�ķ�����Ϊ$\overrightarrow{n}$=��x��y��z����$\overrightarrow{BE}$=$��-2��\sqrt{2}��0��$��$\overrightarrow{BF}$=$��-2�ˣ�2\sqrt{2}-2\sqrt{2}�ˣ�2�ˣ�$��
��$\left\{\begin{array}{l}{-2x+\sqrt{2}y=0}\\{-2��x+��2\sqrt{2}-2\sqrt{2}�ˣ�y+2��z=0}\end{array}\right.$��
ȡ$\overrightarrow{n}$=$���ˣ�\sqrt{2}�ˣ�3��-2��$��
�֡�ƽ��BEC�ķ�����Ϊ$\overrightarrow{m}$=��0��0��1����
��cos45��=$\frac{|3��-2|}{\sqrt{3{��}^{2}+��3��-2��^{2}}}$=$\frac{\sqrt{2}}{2}$����Ϊ3��2-6��+2=0��
��æ�=1$��\frac{\sqrt{3}}{3}$��
�֡�0���ˣ�1��
���=1-$\frac{\sqrt{3}}{3}$��
���� ���⿼���˿ռ�λ�ù�ϵ���ռ�ǡ���������Ӧ�á������нǹ�ʽ���������������ʣ�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | c��a��b | B�� | a��c��b | C�� | a��b��c | D�� | b��a��c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������DZ�Ҫ���� | B�� | ��Ҫ�������dz������ | ||
| C�� | ��ֱ�Ҫ���� | D�� | �dz��������Ҳ�DZ�Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2��a��1 | B�� | -2��a��1 | C�� | 1��a��2 | D�� | 1��a��2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com