
分析 按三种不同方式展开长方体的侧面,计算平面图形中三条线段的长,比较得结论.
解答 解:长方体ABCD-A1B1C1D1的表面可如图三种方法展开后,A、C1两点间的距离分别为: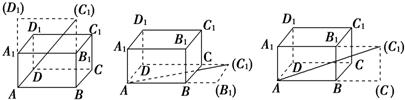
$\sqrt{(1+2)^{2}+{3}^{2}}$=3$\sqrt{2}$,
$\sqrt{(3+1)^{2}+{2}^{2}}$=2$\sqrt{5}$,
$\sqrt{(3+2)^{2}+{1}^{2}}$=$\sqrt{26}$.
三者比较得3$\sqrt{2}$是从点A沿表面到C1的最短距离.
故答案为:3$\sqrt{2}$.
点评 本题考查棱柱的结构特征,考查分类讨论思想,考查计算能力,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2) | C. | [0,2) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b>c+d⇒a>c且b>d | B. | ac2>bc2⇒a>b | ||
| C. | $\frac{c}{a}$>$\frac{b}{d}$⇒ab<cd | D. | $\sqrt{a}$>$\sqrt{b}$?a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
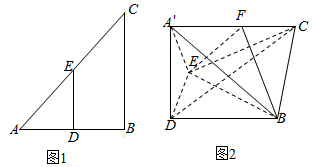 如图1在Rt△ABC中,∠ABC=90°,D、E分别为线段AB、AC的中点,AB=4,BC=2$\sqrt{2}$.以DE为折痕,将Rt△ADE折起到图2的位置,使平面A′DE⊥平面DBCE,连接A′C,′B,设F是线段A′C上的动点,满足$\overrightarrow{CF}$=λ$\overrightarrow{CA′}$.
如图1在Rt△ABC中,∠ABC=90°,D、E分别为线段AB、AC的中点,AB=4,BC=2$\sqrt{2}$.以DE为折痕,将Rt△ADE折起到图2的位置,使平面A′DE⊥平面DBCE,连接A′C,′B,设F是线段A′C上的动点,满足$\overrightarrow{CF}$=λ$\overrightarrow{CA′}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com