
分析 函数y=f(x+2016)的图象是将y=f(x)像左平移2016个单位得到的,要使任意的x∈R,恒有f(x+2016)>f(x),只需f(x+2016)的图象恒在f(x)的图象上方,据此列出关于a的不等式解出来即可.
解答 解:当a>0,x>0时,该函数图象过原点,关于x=a对称,顶点为(a,-a),
结合该函数还是奇函数,图象关于原点对称.
而函数y=f(x+2016)的图象是将y=f(x)像左平移2016个单位得到的,
要使任意的x∈R,恒有f(x+2016)>f(x),
只需f(x+2016)的图象恒在f(x)的图象上方,
所以只需y=f(x+2016)与x轴最右边的交点在A(2a-2016,0)
在y=f(x)与x轴最左边交点B(-2a,0)的左边,
因此应该有2a-2016<-2a,解得0<a<504.
a≤0时,x>0,f(x)=x,函数f(x)是定义在R上的奇函数,
∴f(x)=x,
∴?x∈R,f(x+2016)>f(x),
综上所述,a<504.
故答案为:a<504.
点评 这道题是将不等式恒成立问题转化为函数的最值问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b>c+d⇒a>c且b>d | B. | ac2>bc2⇒a>b | ||
| C. | $\frac{c}{a}$>$\frac{b}{d}$⇒ab<cd | D. | $\sqrt{a}$>$\sqrt{b}$?a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
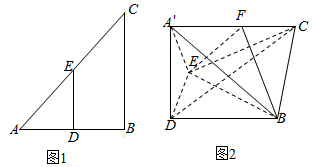 如图1在Rt△ABC中,∠ABC=90°,D、E分别为线段AB、AC的中点,AB=4,BC=2$\sqrt{2}$.以DE为折痕,将Rt△ADE折起到图2的位置,使平面A′DE⊥平面DBCE,连接A′C,′B,设F是线段A′C上的动点,满足$\overrightarrow{CF}$=λ$\overrightarrow{CA′}$.
如图1在Rt△ABC中,∠ABC=90°,D、E分别为线段AB、AC的中点,AB=4,BC=2$\sqrt{2}$.以DE为折痕,将Rt△ADE折起到图2的位置,使平面A′DE⊥平面DBCE,连接A′C,′B,设F是线段A′C上的动点,满足$\overrightarrow{CF}$=λ$\overrightarrow{CA′}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com