
分析 (1)利用代入法求点D的轨迹E的方程;
(2)设直线MN的方程为x=ty+2a联立得y2-4aty-8a2=0,利用韦达定理,证明$\overrightarrow{OM}•\overrightarrow{ON}$<0,即可得出结论.
解答 解:(1))设D(x,y),P(m,n)$\left\{\begin{array}{l}x=\frac{2a+m}{2}\\ y=\frac{n}{2}\end{array}\right.$…(1分)
所以$\left\{\begin{array}{l}m=2x-2a\\ n=2y\end{array}\right.$…(2分)
又(m+2a)2+n2=4a2…(3分)
所以所求方程为x2+y2=a2…(4分)
(2)轨迹E与x轴正半轴的交点F(a,0)…(5分)
抛物线C的方程为y2=4ax…(6分)
设$M(\frac{y_1^2}{4a},{y_1})$,$N(\frac{y_2^2}{4a},{y_2})$,设直线MN的方程为x=ty+2a
联立得y2-4aty-8a2=0,
则$\left\{\begin{array}{l}{y_1}+{y_2}=4at\\{y_1}{y_2}=-8{a^2}\end{array}\right.$…(8分)
所以$\overrightarrow{OM}•\overrightarrow{ON}={x_1}{x_2}+{y_1}{y_2}=\frac{y_1^2}{4a}•\frac{y_2^2}{4a}+{y_1}{y_2}=-4{a^2}<0$…(10分)
所以坐标原点在以MN为直径的圆内…(12分)
点评 本题考查代入法求轨迹方程,考查直线与抛物线的位置关系,考查向量知识的运用,正确运用向量知识、韦达定理是关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 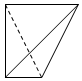 | C. | 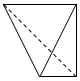 | D. | 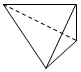 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com