
一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、4、5,现从盒子中随机抽取卡片.
(1)从盒中依次抽取两次卡片,每次抽取一张,取出的卡片不放回,求两次取到的卡片的数字既不全是奇数,也不全是偶数的概率;
(2)若从盒子中有放回的抽取3次卡片,每次抽取一张,求恰有两次取到卡片的数字为偶数的概率;
(3)从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当抽到记有奇数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望.
(1) ;(2)
;(2)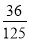 ;
;
(3)
X | 1 | 2 | 3 |
P |
|
|
|
E(X)=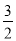
【解析】
试题分析:(1)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(2)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;求随机变量的分布列的主要步骤:一是明确随机变量的取值,并确定随机变量服从何种概率分布;二是求每一个随机变量取值的概率,三是列成表格;(3)求出分布列后注意运用分布列的两条性质检验所求的分布列是否正确;(4)求解离散随机变量分布列和方差,首先要理解问题的关键,其次要准确无误的找出随机变量的所有可能值,计算出相对应的概率,写成随机变量的分布列,正确运用均值、方差公式进行计算.
试题解析:(1)因为1,3,5是奇数,2,4是偶数,
设事件A为“两次取到的卡片的数字既不全是奇数,也不全是偶数”
P(A)=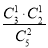 =
=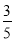 或P(A)=1-
或P(A)=1-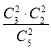 =
=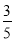 .
.
设B表示事件“有放回地抽取3次卡片,每次抽取一张,恰有两次取到的卡片上数字为偶数”,由已知,每次取到的卡片上数字为偶数的概率为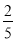 ,
,
则P(B)= ·(
·(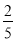 )2·(1-
)2·(1-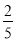 )=
)=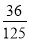 .
.
(3)依题意,X的可能取值为1,2,3.
P(X=1)=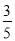 ,P(X=2)=
,P(X=2)=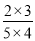 =
=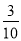 ,P(X=3)=
,P(X=3)=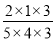 =
=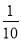 ,
,
所以X的分布列为
X | 1 | 2 | 3 |
P |
|
|
|
E(X)=1×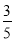 +2×
+2×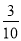 +3×
+3×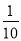 =
=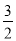 .
.
考点:利用古典概型求随机事件的概率以及随机变量的分布列和期望.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源:2015届福建省高二下学期期中考理科数学试卷(解析版) 题型:解答题
设 是函数
是函数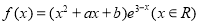 的一个极值点.
的一个极值点.
(1)求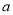 与
与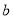 的关系式(用
的关系式(用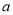 表示
表示 );
);
(2)求 的单调区间;
的单调区间;
(3)设 ,若存在
,若存在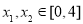 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
对于任意给定的实数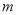 ,直线
,直线 与双曲线
与双曲线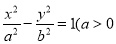 ,
,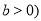 最多有一个交点则,双曲线的离心率等于
最多有一个交点则,双曲线的离心率等于
A.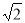 B.
B.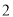 C.
C.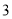 D.
D.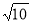
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:选择题
随机变量X的概率分布规律为P(X=n)=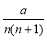 (n=1,2,3,4),其中a是常数,
(n=1,2,3,4),其中a是常数,
则P( <X<
<X<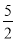 )的值为( )
)的值为( )
A.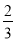 B.
B.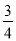 C.
C.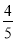 D.
D.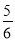
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考理科数学试卷(解析版) 题型:解答题
设函数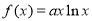
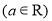 ,已知曲线
,已知曲线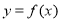 在点
在点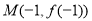 处的切线方程是
处的切线方程是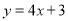 .
.
(1)求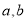 的值;并求出函数的单调区间;
的值;并求出函数的单调区间;
(2)求函数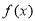 在区间
在区间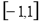 上的最值.
上的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com