
设 是函数
是函数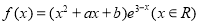 的一个极值点.
的一个极值点.
(1)求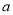 与
与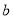 的关系式(用
的关系式(用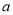 表示
表示 );
);
(2)求 的单调区间;
的单调区间;
(3)设 ,若存在
,若存在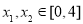 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)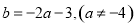 ;
;
(2)① 当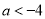 时,单调递增区间为:
时,单调递增区间为: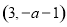 ;单调递减区间为:
;单调递减区间为: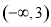 ,
,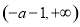 ;
;
② 当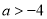 时,单调递增区间为:
时,单调递增区间为: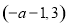 ;单调递减区间为:
;单调递减区间为: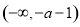 ,
,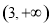 ;
;
(3)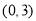 .
.
【解析】
试题分析:(1)解决类似的问题时,注意区分函数的最值和极值.求函数的最值时,要先求函数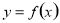 在区间
在区间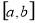 内使
内使 的点,再计算函数
的点,再计算函数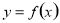 在区间内所有使
在区间内所有使 的点和区间端点处的函数值,最后比较即得.(2)第二问关键是分离参数,把所求问题转化为求函数的最小值问题.(3)若可导函数
的点和区间端点处的函数值,最后比较即得.(2)第二问关键是分离参数,把所求问题转化为求函数的最小值问题.(3)若可导函数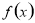 在指定的区间
在指定的区间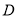 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为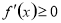
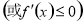 恒成立,从而构建不等式,要注意“=”是否可以取到.
恒成立,从而构建不等式,要注意“=”是否可以取到.
试题解析:(1)∵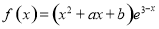
∴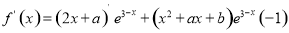
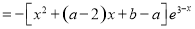
由题意得: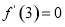 ,即
,即 ,
,
∴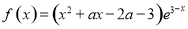 且
且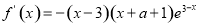
令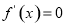 得
得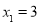 ,
,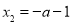
∵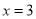 是函数
是函数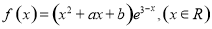 的一个极值点.
的一个极值点.
∴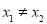 ,即
,即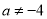 故
故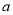 与
与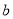 的关系式
的关系式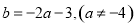
(2) ① 当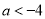 时,
时,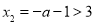 ,由
,由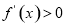 得单调递增区间为:
得单调递增区间为: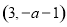 ;
;
由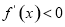 得单调递减区间为:
得单调递减区间为: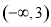 ,
,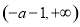 ;
;
② 当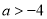 时,
时,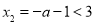 ,由
,由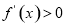 得单调递增区间为:
得单调递增区间为: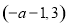 ;
;
由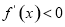 得单调递减区间为:
得单调递减区间为: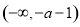 ,
,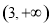 ;
;
(3) 由(2)知:当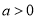 时,
时,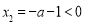 ,
,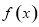 在
在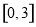 上单调递增,在
上单调递增,在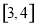 上单调递减,
上单调递减,
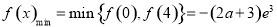 ,
,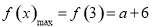
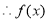 在
在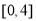 上的值域为
上的值域为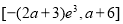
易知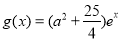 在
在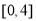 上是增函数
上是增函数
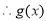 在
在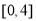 上的值域为
上的值域为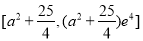
由于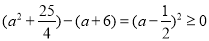 ,又因为要存在
,又因为要存在 ,
,
使得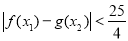 成立,所以必须且只须
成立,所以必须且只须 , 解得:
, 解得: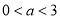
所以: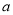 的取值范围为
的取值范围为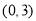
考点:(1)利用导数求函数的最值;(2)利用导数研究函数的单调性.(3)函数的恒成立问题.


科目:高中数学 来源:2015届福建省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
观察 ,
,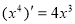 ,
,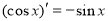 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在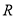 上的函数
上的函数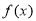 满足
满足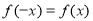 ,记
,记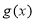 为
为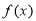 的导函数,则
的导函数,则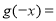 ( )
( )
A.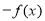 B.
B.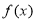 C.
C.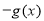 D.
D.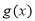
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考理科数学试卷(解析版) 题型:选择题
某车间加工零件的数量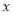 与加工时间
与加工时间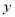 的统计数据如下表:
的统计数据如下表:
零件数 | 10 | 20 | 30 |
加工时间 | 21 | 30 | 39 |
现已求得上表数据的回归方程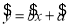 中的
中的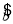 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为
A.84分钟 B.94分钟 C.102分钟 D.112分钟
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:解答题
一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、4、5,现从盒子中随机抽取卡片.
(1)从盒中依次抽取两次卡片,每次抽取一张,取出的卡片不放回,求两次取到的卡片的数字既不全是奇数,也不全是偶数的概率;
(2)若从盒子中有放回的抽取3次卡片,每次抽取一张,求恰有两次取到卡片的数字为偶数的概率;
(3)从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当抽到记有奇数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com