
【题目】如图,四边形![]() 为菱形,且
为菱形,且![]() ,
,![]() ,
,![]() ,点
,点![]() 在面
在面![]() 上的投影
上的投影![]() 恰在
恰在![]() 上,点
上,点![]() 为
为![]() 中点.
中点.
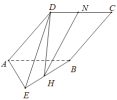
(1)求证:![]() 为线段
为线段![]() 的中点;
的中点;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,证明点
,证明点![]() 为
为![]() 中点.又利用
中点.又利用![]() 面
面![]() ,证得
,证得![]() ,结合条件
,结合条件![]() ,即可证明
,即可证明![]() 面
面![]() ,从而得到
,从而得到![]() ,证明
,证明![]() 是中位线,即可证明
是中位线,即可证明![]() 为线段
为线段![]() 的中点;
的中点;
(2)建立空间直角坐标系,写出各点的坐标,分别求出平面![]() 的一个法向量
的一个法向量![]() 以及平面
以及平面![]() 的一个法向量
的一个法向量![]() ,再求出两个法向量的夹角的余弦,通过观察得二面角与两法向量夹角相等,则可得结论..
,再求出两个法向量的夹角的余弦,通过观察得二面角与两法向量夹角相等,则可得结论..
(1)证明:过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
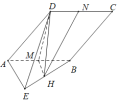
由菱形![]() ,
,![]() ,及
,及![]() ,
,
可知![]() ,
,![]() 为
为![]() 中点,
中点,
![]() 面
面![]() ,
,![]() ,
,
又![]() ,
,![]() 面
面![]() ,
,
![]() 面
面![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
由![]() 为
为![]() 中点,可知,
中点,可知,![]() 为线段
为线段![]() 的中点;
的中点;
(2)以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 所在直线为
所在直线为![]() 轴,
轴,
过![]() 平行
平行![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
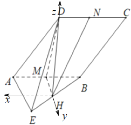
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
设面![]() 的一个法向量
的一个法向量![]() ,
,
![]() ,
,![]() ,
,
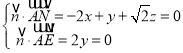 ,取
,取![]()
设面![]() 的一个法向量
的一个法向量![]() ,
,
![]() ,
,![]() ,
,
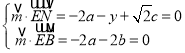 ,取
,取![]() ,
,
∴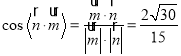 ,
,
二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,曲线
轴的正半轴重合,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是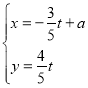 (
(![]() 为参数).
为参数).
(1)若![]() ,
,![]() 是圆
是圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离
的距离![]() 的最小值和最大值;
的最小值和最大值;
(2)直线![]() 与
与![]() 关于原点对称,且直线
关于原点对称,且直线![]() 截曲线
截曲线![]() 的弦长等于
的弦长等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家正积极推行垃圾分类工作,教育部办公厅等六部门也发布了《关于在学校推进生活垃圾分类管理工作的通知》.《通知》指出,到2020年底,各学校生活垃圾分类知识普及率要达到100%某市教育主管部门据此做了“哪些活动最能促进学生进行垃圾分类”的问卷调查(每个受访者只能在问卷的4个活动中选择一个)如图是调查结果的统计图,以下结论正确的是( )
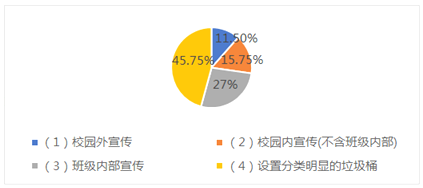
A.回答该问卷的受访者中,选择的(2)和(3)人数总和比选择(4)的人数多
B.回该问卷的受访者中,选择“校园外宣传”的人数不是最少的
C.回答该问卷的受访者中,选择(4)的人数比选择(2)的人数可能多30人
D.回答该问卷的总人数不可能是1000人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,AE⊥平面ABCD,PD∥AE,PD=AD=2EA=2,G,F,H分别为BE,BP,PC的中点.
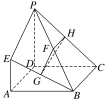
(1)求证:平面ABE⊥平面GHF;
(2)求直线GH与平面PBC所成的角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校准备采用导师制成立培养各学科全优尖子生培优小组![]() ,设想培优小组
,设想培优小组![]() 中,每1名学生需要配备2名理科教师和2名文科教师做导师;设想培优小组
中,每1名学生需要配备2名理科教师和2名文科教师做导师;设想培优小组![]() 中,每1名学生需要配备3名理科教师和1名文科教师做导师.若学校现有14名理科教师和9名文科教师积极支持,则两培优小组能够成立的学生人数和最多是_________.
中,每1名学生需要配备3名理科教师和1名文科教师做导师.若学校现有14名理科教师和9名文科教师积极支持,则两培优小组能够成立的学生人数和最多是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
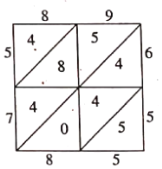
【题目】写算,是一种格子乘法,也是笔算乘法的一种,用以区别筹算与珠算,它由明代数学家吴敬在其撰写的《九章算法比类大全》一书中提出,是从天元式的乘法演变而来.例如计算![]() ,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出
,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出![]() 的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查防疫期间学生居家每天锻炼时间情况,从高一、高二年级学生中分别随机抽取100人,由调查结果得到如下的频率分布直方图:
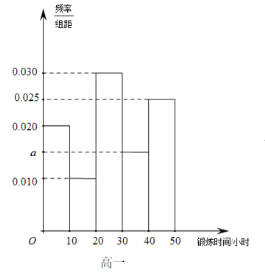
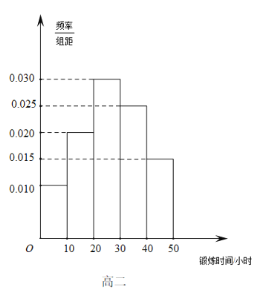
(Ⅰ)写出频率分布直方图(高一)中![]() 的值;记高一、高二学生100人锻炼时间的样本的方差分别为
的值;记高一、高二学生100人锻炼时间的样本的方差分别为![]() ,
,![]() ,试比较
,试比较![]() ,
,![]() 的大小(只要求写出结论);
的大小(只要求写出结论);
(Ⅱ)估计在高一、高二学生中各随机抽取1人,恰有一人的锻炼时间大于20分钟的概率;
(Ⅲ)由频率分布直方图可以认为,高二学生锻炼时间![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差,且每名学生锻炼时间相互独立,设
近似为样本方差,且每名学生锻炼时间相互独立,设![]() 表示从高二学生中随机抽取10人,其锻炼时间位于
表示从高二学生中随机抽取10人,其锻炼时间位于![]() 的人数,求
的人数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区间的中点值作代表,计算得![]()
②若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com