
【题目】对于函数![]() 、
、![]() 、
、![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 、
、![]() 的和谐函数.
的和谐函数.
(1)已知函数![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 是否为
是否为![]() 、
、![]() 的和谐函数?并说明理由;
的和谐函数?并说明理由;
(2)已知![]() 为函数
为函数![]() ,
,![]() 的和谐函数,其中
的和谐函数,其中![]() ,若方程
,若方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 是
是![]() 、
、![]() 的和谐函数(2)
的和谐函数(2)![]()
【解析】
试题分析:(1)h(x)是![]() 、
、![]() 的和谐函数,存在a=-1,b=1,设
的和谐函数,存在a=-1,b=1,设![]() ,利用新定义判断即可.(2)解法一:方程
,利用新定义判断即可.(2)解法一:方程![]() 在x∈[3,9]上有解,即log3(9x)+tlog3(3x)=0在x∈[3,9]上有解,设m=log3x,x∈[3,9],则m∈[1,2],原问题可以转化关于m的方程(1+t)m+(t+2)=0在m∈[1,2]上有解,令g(m)=(1+t)m+(t+2)通过g(1)g(2)≤0,求解即可.解法二:log3(9x)+tlog3(3x)=0,化简得:2+log3x+t(1+log3x)=0,原式可转化为方程
在x∈[3,9]上有解,即log3(9x)+tlog3(3x)=0在x∈[3,9]上有解,设m=log3x,x∈[3,9],则m∈[1,2],原问题可以转化关于m的方程(1+t)m+(t+2)=0在m∈[1,2]上有解,令g(m)=(1+t)m+(t+2)通过g(1)g(2)≤0,求解即可.解法二:log3(9x)+tlog3(3x)=0,化简得:2+log3x+t(1+log3x)=0,原式可转化为方程![]() 在x∈[3,9]区间上有解,即求函数
在x∈[3,9]区间上有解,即求函数![]() 在x∈[3,9]的值域,通过分离常数法,求解即可
在x∈[3,9]的值域,通过分离常数法,求解即可
试题解析:(1) ![]() 是
是![]() 、
、![]() 的生成函数,因为存在
的生成函数,因为存在![]()
使![]()
设![]() ,则
,则![]() ,
,
所以![]() ,
,![]()
所以![]() 是
是![]() 、
、![]() 的和谐函数.
的和谐函数.
(2) 解法一:依题意,由方程![]() 在
在![]() 上有解,即
上有解,即![]() 在
在![]() 上有解,
上有解,
化简得:![]()
设![]() ,
,![]() , 则
, 则![]() ,即
,即 ![]()
原问题可以转化关于![]() 的方程
的方程![]() 在
在![]() 上有解,
上有解,
令![]()
由题意得:![]() , 解得
, 解得![]() .
.
综上:![]()
(2) 解法二:![]() ,化简得:
,化简得:![]()
因为![]() ,所以
,所以![]() ,
,
原式可转化为方程![]() 在
在![]() 区间上有解
区间上有解
即求函数![]() 在
在![]() 的值域
的值域
令![]() ,因为
,因为 ![]()
由反比例函数性质可得 ,函数![]() 的值域为
的值域为![]()
所以实数![]() 的取值范围
的取值范围![]()


科目:高中数学 来源: 题型:
【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.

(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(I)曲线![]() 在x=1处的切线与直线
在x=1处的切线与直线![]() 垂直,求实数a的值;
垂直,求实数a的值;
(II)当![]() 时,求证:
时,求证: ![]() 在(1,+∞)上单调递增;
在(1,+∞)上单调递增;
(III)当x≥1时, ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间四边形ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC是( )
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查市民对汽车品牌的认可度,在秋季车展上,从有意购车的500名市民中,随机抽样100名市民,按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2.频率分布表Ⅰ
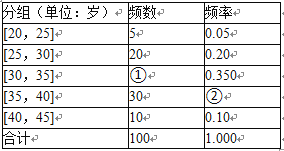
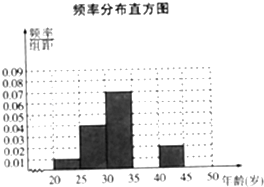
(1)频率分布表中的①②位置应填什么数?并补全频率分布直方图,再根据频率分布直方图统计这500名志愿者得平均年龄;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加的宣传活动,再从这20名中选取2名志愿者担任主要发言人.记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数字序列:3,-2,-4,0,5,13,6,-32,-18,9,-20.下面是从该序列中搜索所有负数的一个算法,请补全步骤:
S1 输入实数a;
S2 _____;
S3 输出a,转S1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中:
①在回归分析中, 可用相关指数![]() 的值判断的拟合效果,
的值判断的拟合效果,![]() 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近![]() ;
;
③若数据![]() 的方差为
的方差为![]() ,则
,则![]() 的方差为
的方差为![]() ;
;
④对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
其中真命题的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com