
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,函数
,函数![]() ,若存在
,若存在![]() 、
、![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由![]() 可得出
可得出![]() ,令
,令![]() 得出
得出![]() ,
,![]() ,然后讨论
,然后讨论![]() 与
与![]() 的大小关系,结合导数可得出函数
的大小关系,结合导数可得出函数![]() 的单调增区间和减区间;
的单调增区间和减区间;
(2)利用导数求得函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,利用二次函数的基本性质得出函数
,利用二次函数的基本性质得出函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,由此可得出
,由此可得出![]() ,进而可解得实数
,进而可解得实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
由题意可知,![]() ,则
,则![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,![]() .
.
因为![]() 是函数
是函数![]() 的极值点,所以
的极值点,所以![]() ,即
,即![]() .
.
①当![]() 时,即当
时,即当![]() 时,解不等式
时,解不等式![]() ,得
,得![]() 或
或![]() ;解不等式
;解不等式![]() ,解得
,解得![]() .
.
此时,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
②当![]() 时,即当
时,即当![]() 时,解不等式
时,解不等式![]() ,得
,得![]() 或
或![]() ;解不等式
;解不等式![]() ,解得
,解得![]() .
.
此时,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 为减函数,
为减函数,
所以,函数![]() 的最大值为
的最大值为![]() ,
,
因为函数![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,
所以,函数![]() 的最小值为
的最小值为![]() ,
,
所以,![]() 在
在![]() 上恒成立.
上恒成立.
要使存在![]() 、
、![]() ,使得
,使得![]() 成立,
成立,
只需要![]() ,即
,即![]() ,所以
,所以![]() .
.
又因为![]() ,所以实数
,所以实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

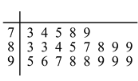
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆![]() 是某个旅游景点的平面示意图,为了保护景点和方便游客观赏,管理部门规划从公路
是某个旅游景点的平面示意图,为了保护景点和方便游客观赏,管理部门规划从公路![]() 上某点
上某点![]() 起修建游览线路
起修建游览线路![]() ,
,![]() 、
、![]() 、
、![]() 分别与半圆相切,且四边形
分别与半圆相切,且四边形![]() 是等腰梯形.已知半圆半径
是等腰梯形.已知半圆半径![]() 百米,每修建1百米游览道路需要费用为20万元,设
百米,每修建1百米游览道路需要费用为20万元,设![]() 与圆的切点为
与圆的切点为![]() ,
,![]() (单位:弧度).
(单位:弧度).
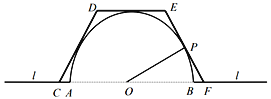
(1)试将修建游览道路所需费用![]() 表示为
表示为![]() 的函数;
的函数;
(2)试求修建游览道路所需最少费用为多少万元?(精确到0.1,参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)设直线l为函数![]() 的图象上一点
的图象上一点![]() 处的切线,证明:在区间
处的切线,证明:在区间![]() 上存在唯一的
上存在唯一的![]() ,使得直线l与曲线
,使得直线l与曲线![]() 相切并求出此时n的值.(参考数据:
相切并求出此时n的值.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在圆心角为直角,半径为![]() 的扇形区域内进行野外生存训练.如图所示,在相距
的扇形区域内进行野外生存训练.如图所示,在相距![]() 的
的![]() ,
,![]() 两个位置分别为300,100名学生,在道路
两个位置分别为300,100名学生,在道路![]() 上设置集合地点
上设置集合地点![]() ,要求所有学生沿最短路径到
,要求所有学生沿最短路径到![]() 点集合,记所有学生进行的总路程为
点集合,记所有学生进行的总路程为![]() .
.
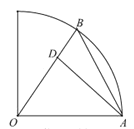
(1)设![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当![]() 最小时,集合地点
最小时,集合地点![]() 离点
离点![]() 多远?
多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com