
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

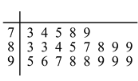
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面
的底面![]() 是矩形,
是矩形,![]() 底面
底面![]() ,且
,且![]() ,设E、F、G分别为PC、BC、CD的中点,H为EG的中点,如图.
,设E、F、G分别为PC、BC、CD的中点,H为EG的中点,如图.
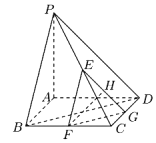
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线FH与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为准备参加市运动会,对本校甲、乙两个田径队中![]() 名跳高运动员进行了测试,并用茎叶图表示出本次测试
名跳高运动员进行了测试,并用茎叶图表示出本次测试![]() 人的跳高成绩(单位:
人的跳高成绩(单位:![]() ).跳高成绩在
).跳高成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
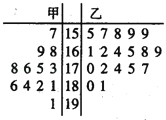
(1)求甲队队员跳高成绩的中位数;
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取![]() 人,则
人,则![]() 人中“合格”与“不合格”的人数各为多少;
人中“合格”与“不合格”的人数各为多少;
(3)若从所有“合格”运动员中选取![]() 名,用
名,用![]() 表示所选运动员中能参加市运动会开幕式旗林队的人数,试求
表示所选运动员中能参加市运动会开幕式旗林队的人数,试求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足“对任意正整数
满足“对任意正整数![]() ,都存在正整数
,都存在正整数![]() ,使得
,使得![]() ”,则称数列
”,则称数列![]() 具有“性质
具有“性质![]() ”.已知数列
”.已知数列![]() 为无穷数列.
为无穷数列.
(1)若![]() 为等比数列,且
为等比数列,且![]() ,判断数列
,判断数列![]() 是否具有“性质
是否具有“性质![]() ”,并说明理由;
”,并说明理由;
(2)若![]() 为等差数列,且公差
为等差数列,且公差![]() ,求证:数列
,求证:数列![]() 不具有“性质
不具有“性质![]() ”;
”;
(3)若等差数列![]() 具有“性质
具有“性质![]() ”,且
”,且![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为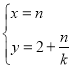 (
(![]() 为参数).设直线
为参数).设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时的点
变化时的点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设射线
轴正半轴为极轴建立极坐标系,设射线![]() 的极坐标方程为
的极坐标方程为![]() 且
且![]() ,点
,点![]() 是射线
是射线![]() 与曲线
与曲线![]() 的交点,求点
的交点,求点![]() 的极径.
的极径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com