
【题目】已知数列{an}满足![]() .
.
(1)求a1,a2,a3的值;
(2)对任意正整数n,an小数点后第一位数字是多少?请说明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)a1,a2小数点后第一位数字均为5,当n≥3,n∈N*时,an小数点后第一位数字均为6.见解析
;(2)a1,a2小数点后第一位数字均为5,当n≥3,n∈N*时,an小数点后第一位数字均为6.见解析
【解析】
(1)因为数列{an}满足![]() ,令n=1,n=2,n=3,分别求解.
,令n=1,n=2,n=3,分别求解.
(2)根据a1,a2小数点后第一位数字均为5,a3小数点后第一位数字为6,猜想对任意正整数n(n≥3),均有0.6<an<0.7,根据![]() ,所以对任意正整数n(n≥3),有an≥a3>0.6,只要证明:对任意正整数n(n≥3),有
,所以对任意正整数n(n≥3),有an≥a3>0.6,只要证明:对任意正整数n(n≥3),有![]() 即可.采用数学归纳法证明.
即可.采用数学归纳法证明.
(1)a1![]() ,a2
,a2![]() ;a3
;a3![]() ,
,
可得![]() ,
,![]() ,
,![]() ;
;
(2)a1,a2小数点后第一位数字均为5,a3小数点后第一位数字为6,
下证:对任意正整数n(n≥3),均有0.6<an<0.7,
注意到![]() ,
,
故对任意正整数n(n≥3),有an≥a3>0.6,
下用数学归纳法证明:对任意正整数n(n≥3),有![]()
①当n=3时,有![]() ,命题成立;
,命题成立;
②假设当n=k(k∈N*,k≥3)时,命题成立,即![]()
则当n=k+1时,![]()
∵![]()
∴![]() ∴
∴![]()
∴n=k+1时,命题也成立;
综合①②,任意正整数n(n≥3),![]() .
.
由此,对正整数n(n≥3),0.6<an<0.7,此时an小数点后第一位数字均为6.
所以a1,a2小数点后第一位数字均为5,当n≥3,n∈N*时,an小数点后第一位数字均为6.


科目:高中数学 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明![]() 如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形
如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形![]() 若直角三角形中较小的锐角
若直角三角形中较小的锐角![]() ,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是
,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

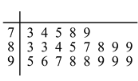
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
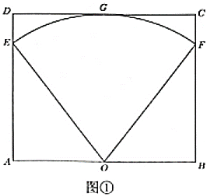
【题目】某公园计划在矩形空地上建造一个扇形花园如图①所示,矩形![]() 的
的![]() 边与
边与![]() 边的长分别为48米与40米,扇形的圆心
边的长分别为48米与40米,扇形的圆心![]() 为
为![]() 中点,扇形的圆弧端点
中点,扇形的圆弧端点![]() ,
,![]() 分别在
分别在![]() 与
与![]() 上,圆弧的中点
上,圆弧的中点![]() 在
在![]() 上.
上.
(1)求扇形花园的面积(精确到1平方米);
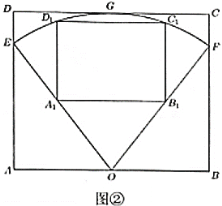
(2)若在扇形花园内开辟出一个矩形区域![]() 为花卉展览区.如图②所示,矩形
为花卉展览区.如图②所示,矩形![]() 的四条边与矩形
的四条边与矩形![]() 的对应边平行,点
的对应边平行,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,点
上,点![]() ,
,![]() 在扇形的弧上.某同学猜想:当矩形
在扇形的弧上.某同学猜想:当矩形![]() 面积最大时,两矩形
面积最大时,两矩形![]() 与
与![]() 的形状恰好相同(即长与宽之比相同),试求花卉展览区
的形状恰好相同(即长与宽之比相同),试求花卉展览区![]() 面积的最大值,并判断上述猜想是否正确(请说明理由).
面积的最大值,并判断上述猜想是否正确(请说明理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点是椭圆
的顶点是椭圆![]() 的中心,焦点与该椭圆的右焦点重合.
的中心,焦点与该椭圆的右焦点重合.
(1)求抛物线![]() 的方程;
的方程;
(2)已知动直线![]() 过点
过点![]() ,交抛物线
,交抛物线![]() 于
于![]() ,
,![]() 两点,坐标原点
两点,坐标原点![]() 为
为![]() 的中点,求证
的中点,求证![]() ;
;
(3)在(2)的条件下,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以
被以![]() 为直径的圆所截得的弦长恒为定值?如果存在,求出
为直径的圆所截得的弦长恒为定值?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
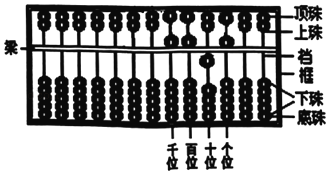
【题目】珠算被誉为中国的第五大发明,最早见于汉朝徐岳撰写的《数术记遗》2013年联合国教科文组织正式将中国珠算项目列入教科文组织人类非物质文化遗产.如图,我国传统算盘每一档为两粒上珠,五粒下珠,也称为“七珠算盘”.未记数(或表示零)时,每档的各珠位置均与图中最左档一样;记数时,要拨珠靠梁,一个上珠表示“5”,一个下珠表示“1”,例如:当千位档一个上珠、百位档一个上珠、十位档一个下珠、个位档一个上珠分别靠梁时,所表示的数是5515.现选定“个位档”、“十位档”、“百位档”和“千位档”,若规定每档拨动一珠靠梁(其它各珠不动),则在其可能表示的所有四位数中随机取一个数,这个数能被3整除的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com