
【题目】如图,已知抛物线![]() ,直线
,直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,
两点,![]() 是抛物线外一点,连接
是抛物线外一点,连接![]() ,
,![]() 分别交抛物线于点
分别交抛物线于点![]() ,
,![]() ,且
,且![]() .
.
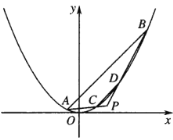
(Ⅰ)若![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】某学校为准备参加市运动会,对本校甲、乙两个田径队中![]() 名跳高运动员进行了测试,并用茎叶图表示出本次测试
名跳高运动员进行了测试,并用茎叶图表示出本次测试![]() 人的跳高成绩(单位:
人的跳高成绩(单位:![]() ).跳高成绩在
).跳高成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
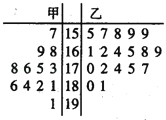
(1)求甲队队员跳高成绩的中位数;
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取![]() 人,则
人,则![]() 人中“合格”与“不合格”的人数各为多少;
人中“合格”与“不合格”的人数各为多少;
(3)若从所有“合格”运动员中选取![]() 名,用
名,用![]() 表示所选运动员中能参加市运动会开幕式旗林队的人数,试求
表示所选运动员中能参加市运动会开幕式旗林队的人数,试求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(sinx+cosx)2![]() cos(2x+π).
cos(2x+π).
(1)求函数f(x)的最小正周期;
(2)已知△ABC的内角A,B,C的对边分别为a,b,c,若![]() ,且a=2,求△ABC的面积.
,且a=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蜂巢是由工蜂分泌蜂蜡建成的.从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成.如图,在正六棱柱![]() 的三个顶点
的三个顶点![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构,如下图(4)所示,
,就形成了蜂巢的结构,如下图(4)所示,
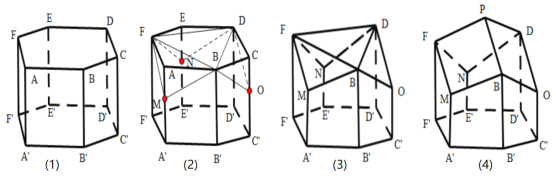
瑞士数学家克尼格利用微积分的方法证明了蜂巢的这种结构是在相同容积下所用材料最省的,英国数学家麦克劳林通过计算得到菱形的一个内角为![]() ,即
,即![]() .以下三个结论①
.以下三个结论①![]() ;②
;② ![]()
![]()
![]() ;③
;③![]() 四点共面,正确命题的个数为______个;若
四点共面,正确命题的个数为______个;若![]() ,
,![]() ,
,![]() ,则此蜂巢的表面积为_______.
,则此蜂巢的表面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为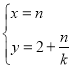 (
(![]() 为参数).设直线
为参数).设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时的点
变化时的点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设射线
轴正半轴为极轴建立极坐标系,设射线![]() 的极坐标方程为
的极坐标方程为![]() 且
且![]() ,点
,点![]() 是射线
是射线![]() 与曲线
与曲线![]() 的交点,求点
的交点,求点![]() 的极径.
的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“国”、“富”、“民”、“强”四个字,有放回地从中任取一张卡片,将三次抽取后“国”“富”两个字都取到记为事件A,用随机模拟的方法估计事件A发生的概率,利用电脑随机产生整数0,1,2,3四个随机数,分别代表“国”、“富”、“民”、“强”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
231 | 232 | 210 | 023 | 122 | 021 | 321 | 220 | 031 |
231 | 103 | 133 | 132 | 001 | 320 | 123 | 130 | 233 |
由此可以估计事件A发生的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
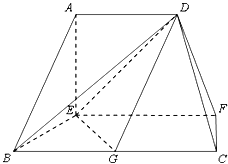
(Ⅰ)求证:AB∥平面DEG;
(Ⅱ)求证:BD⊥EG;
(Ⅲ)求多面体ADBEG的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com