
����Ŀ�������������ſ�Ƭ���ֱ�д�С���������������������ǿ���ĸ��֣��зŻصش�����ȡһ�ſ�Ƭ�������γ�ȡ���������������ֶ�ȡ����Ϊ�¼�A�������ģ��ķ��������¼�A�����ĸ��ʣ����õ��������������0��1��2��3�ĸ���������ֱ��������������������������ǿ�����ĸ��֣���ÿ���������Ϊһ�飬��ʾȡ��Ƭ���εĽ���������ģ�����������18���������
231 | 232 | 210 | 023 | 122 | 021 | 321 | 220 | 031 |
231 | 103 | 133 | 132 | 001 | 320 | 123 | 130 | 233 |
�ɴ˿��Թ����¼�A�����ĸ���Ϊ_____.
���𰸡�![]()
��������
�����ģ�����������18��������������оٷ���������¼�A�������������6�����ɴ��ܹ����¼�A�����ĸ���.
�����⣬�����������ſ�Ƭ���ֱ�д����������������������������ǿ���ĸ��֣�
�зŻصش�����ȡһ�ſ�Ƭ�������γ�ȡ�������������������ֶ�ȡ����Ϊ�¼�A��
�����ģ��ķ��������¼�A�����ĸ��ʣ�
���õ��������������0��1��2��3�ĸ��������
�ֱ������������������������������ǿ�����ĸ��֣�
��ÿ���������Ϊһ�飬��ʾȡ��Ƭ���εĽ���������ģ�����������18���������
�����¼�A������������У�210��021��031��103��001��130����6����
���Թ����¼�A�����ĸ���ΪP![]() .
.
�ʴ�Ϊ��![]() .
.


 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ƻ��ھ��οյ��Ͻ���һ�����λ���ͼ����ʾ������![]() ��
��![]() ����
����![]() �ߵij��ֱ�Ϊ48����40�ף����ε�Բ��
�ߵij��ֱ�Ϊ48����40�ף����ε�Բ��![]() Ϊ
Ϊ![]() �е㣬���ε�Բ���˵�
�е㣬���ε�Բ���˵�![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ�Բ�����е�
�ϣ�Բ�����е�![]() ��
��![]() �ϣ�
�ϣ�
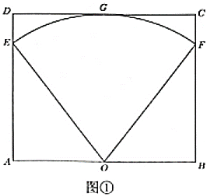
��1�������λ����������ȷ��1ƽ���ף���
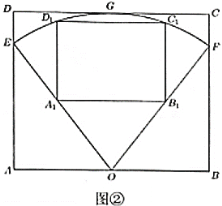
��2���������λ��ڿ��ٳ�һ����������![]() Ϊ����չ��������ͼ����ʾ������
Ϊ����չ��������ͼ����ʾ������![]() �������������
�������������![]() �Ķ�Ӧ��ƽ�У���
�Ķ�Ӧ��ƽ�У���![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() �����εĻ��ϣ�ijͬѧ���룺������
�����εĻ��ϣ�ijͬѧ���룺������![]() ������ʱ��������
������ʱ��������![]() ��
��![]() ����״ǡ����ͬ���������֮����ͬ��������չ����
����״ǡ����ͬ���������֮����ͬ��������չ����![]() ��������ֵ�����ж����������Ƿ���ȷ����˵�����ɣ���
��������ֵ�����ж����������Ƿ���ȷ����˵�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��ֱ��
��ֱ��![]() ����������
����������![]() ��
��![]() ���㣬
���㣬![]() ����������һ�㣬����
����������һ�㣬����![]() ��
��![]() �ֱ��������ڵ�
�ֱ��������ڵ�![]() ��
��![]() ����
����![]() ��
��
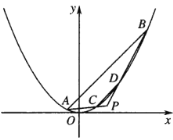
������![]() �����
�����![]() �Ĺ켣���̣�
�Ĺ켣���̣�
������![]() ����
����![]() �������Сֵ��
�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��Ϊ�溯�����ҵ�x��0ʱ��f��x����ex��cosx����ʽf��2x��1��+f��x��2����0�Ľ⼯Ϊ( )
A.��������1��B.��������![]() ��C.��
��C.��![]() ��+����D.��1��+����
��+����D.��1��+����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������״��������![]() ���Ĺ�״�������а�Ĥ��������Ϊ�����ԣ����а����ŽṹΪ��ѧģ�͵�
���Ĺ�״�������а�Ĥ��������Ϊ�����ԣ����а����ŽṹΪ��ѧģ�͵�![]() ��
��![]() ������β��ṹ�а���
������β��ṹ�а���![]() ��
��![]() �Ľṹ������״���������������Ǹ��϶��ɵģ�����Ϊ
�Ľṹ������״���������������Ǹ��϶��ɵģ�����Ϊ![]() .�����н�����ȷ���ǣ� ��
.�����н�����ȷ���ǣ� ��
A.��![]() ����
����![]() Ϊ���ں���
Ϊ���ں���
B.����![]() ��
��![]() ����СֵΪ
����СֵΪ![]()
C.��![]() ������
������![]() ��������������
��������������![]()
D.��![]() ��
��![]() ������
������![]() ����
����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
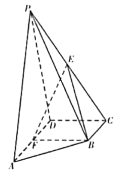
����Ŀ������P��ABCD�У�AB��CD��AB��BC��AB��BC��1��PA��CD��2��PA�͵���ABCD��E��PB��.
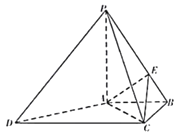
��1��֤����AC��PD��
��2����PE��2BE��������P��ACE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �У�����
�У�����![]() Ϊֱ�����Σ�
Ϊֱ�����Σ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() Ϊ
Ϊ![]() ���е㣬ƽ��
���е㣬ƽ��![]() ����
����![]() .
.
����֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
������![]() �����
�����![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����˾Ϊ����ʵ����Ա���Ľ�����ȫ���᳹���������߹��������Ҫ������ȫ��˾��Χ�ھ���һ���Ҹ��ղ�.Ϊ����Ҫ����669�˵�Ѫ�����л��飬���������϶࣬���߲����ƶ����������ֿɹ�ѡ��ķ���.
����һ����ÿ���˵�Ѫ�ֱ��飬��ʱ��Ҫ��669��.
����������![]() ����һ�����������飬�Ѵ�ÿ��
����һ�����������飬�Ѵ�ÿ��![]() ���˳�����Ѫ�����һ����м��飬���ÿ���˵�Ѫ��Ϊ���ԣ�������Ľ�������ԣ���
���˳�����Ѫ�����һ����м��飬���ÿ���˵�Ѫ��Ϊ���ԣ�������Ľ�������ԣ���![]() ���˵�Ѫ��ֻ�����һ�Σ���ʱ��Ϊÿ���˵�Ѫ����
���˵�Ѫ��ֻ�����һ�Σ���ʱ��Ϊÿ���˵�Ѫ����![]() �Σ��������������ԣ��������
�Σ��������������ԣ��������![]() ���˵�Ѫ���ٷֱ����һ�λ��飬��ʱ����
���˵�Ѫ���ٷֱ����һ�λ��飬��ʱ����![]() ���˵�Ѫ�ܹ���Ҫ����
���˵�Ѫ�ܹ���Ҫ����![]() ��.
��.
����˴��ղ���ÿ���˵�Ѫ����������Եĸ���Ϊ![]() ������Щ��֮������鷴Ӧ�����.
������Щ��֮������鷴Ӧ�����.
��1���跽�����У�ij��![]() ������ÿ���˵�Ѫ�������Ϊ
������ÿ���˵�Ѫ�������Ϊ![]() ����
����![]() �ķֲ���.
�ķֲ���.
��2����![]() ���ԱȽϷ������У�
���ԱȽϷ������У�![]() �ֱ�ȡ2��3��4ʱ�����軯���ƽ���ܴ�������ָ���������ַ�������£���ȷ���һ���������������ƽ�����ٶ��ٴΣ���������������뱣��������
�ֱ�ȡ2��3��4ʱ�����軯���ƽ���ܴ�������ָ���������ַ�������£���ȷ���һ���������������ƽ�����ٶ��ٴΣ���������������뱣��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ������
������![]() ���������������
���������������![]() ��
Ϊ��![]() �۵����С�.
�۵����С�.
��1����![]() ��
��![]() �������
�������![]() ��
��![]() �Ƿ��ǡ�
�Ƿ��ǡ�![]() �۵����С�������ǣ�ָ��m��ֵ��������ǣ���˵�����ɣ�
�۵����С�������ǣ�ָ��m��ֵ��������ǣ���˵�����ɣ�
��2����![]() �������е�ʵ��q��ʹ������
�������е�ʵ��q��ʹ������![]() ��3-�۵����У�
��3-�۵����У�
��3����������![]() ���Ƿ��������
���Ƿ��������![]() ʹ�ö�����
ʹ�ö�����![]() ��
��![]() ����
����![]() �۵����У���
�۵����У���![]() �ĸ�����ǡ��
�ĸ�����ǡ��![]() ����ͬ��ֵ��֤����Ľ���.
����ͬ��ֵ��֤����Ľ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com