
【题目】已知![]() ,
,![]() ,有如下结论:
,有如下结论:
①![]() 有两个极值点;
有两个极值点;
②![]() 有
有![]() 个零点;
个零点;
③![]() 的所有零点之和等于零.
的所有零点之和等于零.
则正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
利用导数分析函数![]() 的单调性,结合零点存在定理可判断命题①的正误;利用导数分析函数
的单调性,结合零点存在定理可判断命题①的正误;利用导数分析函数![]() 的单调性,结合零点存在定理可判断命题②的正误;由
的单调性,结合零点存在定理可判断命题②的正误;由![]() 得出
得出![]() ,设
,设![]() ,由
,由![]() 推导出
推导出![]() ,由此可判断出命题③的正误.综合可得出结论.
,由此可判断出命题③的正误.综合可得出结论.
![]() ,则
,则![]() ,
,![]() .
.
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 单调递增.
单调递增.
所以,函数![]() 的最小值为
的最小值为![]() .
.
![]() ,
,![]() .
.
令![]() ,当
,当![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,
上单调递增,
则![]() ,所以,当
,所以,当![]() 时,
时,![]() .
.
![]() ,
,![]() ,
,
由零点存在定理可知,函数![]() 在
在![]() 和
和![]() 上各有一个零点,
上各有一个零点,
所以,函数![]() 有两个极值点,命题①正确;
有两个极值点,命题①正确;
设函数![]() 的极大值点为
的极大值点为![]() ,极小值点为
,极小值点为![]() ,则
,则![]() ,
,
则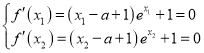 ,所以
,所以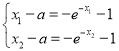 ,
,
函数![]() 的极大值为
的极大值为![]()
![]() ,
,
构造函数![]() ,则
,则![]() ,
,
所以,函数![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]() ,
,![]() ,
,![]() ,则
,则![]() ,即
,即![]() .
.
同理可知,函数![]() 的极小值为
的极小值为![]() .
.
![]() ,
,![]() .
.
由零点存在定理可知,函数![]() 在区间
在区间![]() 、
、![]() 、
、![]() 上各存在一个零点,
上各存在一个零点,
所以,函数![]() 有
有![]() 个零点,命题②正确;
个零点,命题②正确;
令![]() ,得
,得![]() ,
,![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
所以,函数![]() 所有零点之和等于零,命题③正确.
所有零点之和等于零,命题③正确.
故选:D.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是
是![]() 轴上的动点(异于原点
轴上的动点(异于原点![]() ),点
),点![]() 在圆
在圆![]() 上,且
上,且![]() .设线段
.设线段![]() 的中点为
的中点为![]() ,当点
,当点![]() 移动时,记点
移动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
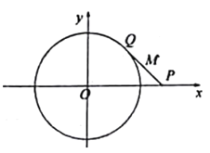
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且点
,且点![]() 在第一象限.
在第一象限.
(ⅰ)求直线![]() 的斜率;
的斜率;
(ⅱ)直线![]() 平行
平行![]() ,交曲线
,交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() .线段
.线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() 、
、![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(sinx+cosx)2![]() cos(2x+π).
cos(2x+π).
(1)求函数f(x)的最小正周期;
(2)已知△ABC的内角A,B,C的对边分别为a,b,c,若![]() ,且a=2,求△ABC的面积.
,且a=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蜂巢是由工蜂分泌蜂蜡建成的.从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成.如图,在正六棱柱![]() 的三个顶点
的三个顶点![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构,如下图(4)所示,
,就形成了蜂巢的结构,如下图(4)所示,
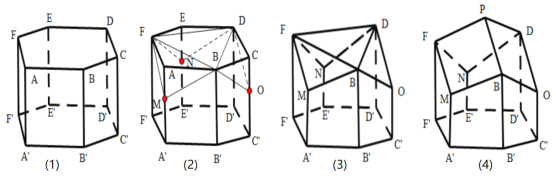
瑞士数学家克尼格利用微积分的方法证明了蜂巢的这种结构是在相同容积下所用材料最省的,英国数学家麦克劳林通过计算得到菱形的一个内角为![]() ,即
,即![]() .以下三个结论①
.以下三个结论①![]() ;②
;② ![]()
![]()
![]() ;③
;③![]() 四点共面,正确命题的个数为______个;若
四点共面,正确命题的个数为______个;若![]() ,
,![]() ,
,![]() ,则此蜂巢的表面积为_______.
,则此蜂巢的表面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD的底面是正方形,![]() 底面ABCD,
底面ABCD,![]() ,E是侧棱的中点.
,E是侧棱的中点.
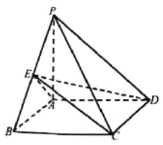
(1)求异面直线AE与PD所成的角;
(2)求点B到平面ECD的距离
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com