Question

19．某班同学参加社会实践活动，对本市25～55岁年龄段的人群进行某项随机调查，得到各年龄段被调查人数的频率分布直方图如图（部分有缺损）：
（1）补全频率分布直方图（需写出计算过程）；
（2）现从[40，55）岁年龄段样本中采用分层抽样方法抽取6人分成A、B两个小组（每组3人）参加户外体验活动，记A组中年龄在[40，45）岁的人数为ξ，
求随机变量ξ的分布列和数学期望Eξ．

Answer 1

分析 （1）第二组的频率为1-（0.04+0.04+0.03+0.02+0.01）×5，作出频率直方图，如右图．
（2）由[40，45）组，[45，50）组和[50，55）组的人数比为0.03：0.02：0.01=3：2：1，
因此三组中抽出的人数分别为3，2，1，ξ=0，1，2，3，利用P（ξ=i）=$\frac{{∁}_{3}^{i}{∁}_{3}^{3-i}}{{∁}_{6}^{3}}$（i=0，1，2，3）即可得出．

解答 解：（1）∵第二组的频率为1-（0.04+0.04+0.03+0.02+0.01）×5=0.3，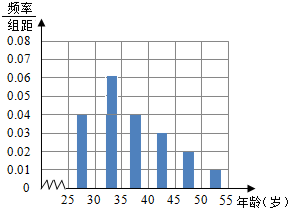
∴高为0.3÷5=0.06．
作出频率直方图，如右图．
（2）∵[40，45）组，[45，50）组和[50，55）组的人数比为0.03：0.02：0.01=3：2：1，
∴三组中抽出的人数分别为3，2，1，
ξ=0，1，2，3，
P（ξ=0）=$\frac{{∁}_{3}^{0}}{{∁}_{6}^{3}}$=$\frac{1}{20}$，P（ξ=1）=$\frac{{∁}_{3}^{1}{∁}_{3}^{2}}{{∁}_{6}^{3}}$=$\frac{9}{20}$，
P（ξ=2）=$\frac{{∁}_{3}^{2}{∁}_{3}^{1}}{{∁}_{6}^{3}}$=$\frac{9}{20}$，P（ξ=3）=$\frac{{∁}_{3}^{3}}{{∁}_{6}^{3}}$=$\frac{1}{20}$，
∴ξ的分布列为：

ξ	0	1	2	3
P	$\frac{1}{20}$	$\frac{9}{20}$	$\frac{9}{20}$	$\frac{1}{20}$

Eξ=$0×\frac{1}{20}$+1×$\frac{9}{20}$+2×$\frac{9}{20}$+3×$\frac{1}{20}$=$\frac{3}{2}$．

点评 本题考查了频率分布直方图、超几何的分布列的概率计算与数学期望，考查了推理能力与计算能力，属于中档题．