
分析 由∠F1PF2为钝角,得到 $\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$<0有解,转化为c2>x02+y02有解,求出x02+y02的最小值后求得椭圆离心率的取值范围.
解答 解:设P(x0,y0),则|x0|<a,
又∠F1PF2为钝角,当且仅当 $\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$<0有解,
即c2>x02+y02有解,即c2>(x02+y02)min.
又y02=b2-$\frac{{b}^{2}}{{a}^{2}}$x02,
∴x02+y02=b2+$\frac{{c}^{2}}{{a}^{2}}$x02∈[b2,a2),
即(x02+y02)min=b2.
故c2>b2,c2>a2-c2,
∴$\frac{{c}^{2}}{{a}^{2}}$>$\frac{1}{2}$,即e>$\frac{\sqrt{2}}{2}$,
又0<e<1,
∴$\frac{\sqrt{2}}{2}$<e<1.
故答案为:$({\frac{{\sqrt{2}}}{2},1})$.
点评 本题考查了直线与圆锥曲线的关系,考查了平面向量数量积在解题中的应用,体现了数学转化思想方法,解答此题的关键在于把存在一点P使∠F1PF2为钝角转化为数量积小于0有解.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
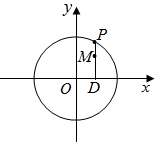 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=$\frac{4}{5}$|PD|.
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=$\frac{4}{5}$|PD|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{7}{2}$ | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如图(部分有缺损):
某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如图(部分有缺损):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com