练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

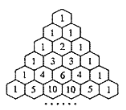
    【题目】“杨辉三角”是我国数学史上的一个伟大成就，是二项式系数在三角形中的一种几何排列.如图所示，去除所有为1的项，依此构成数列2，3，3，4，6，4，5，10，10，5，…，则此数列的前46项和为_____.

    【答案】

    【解析】

    根据“杨辉三角”的特点可知次二项式的二项式系数对应“杨辉三角”中的第行，从而得到第行去掉所有为的项的各项之和为：；根据每一行去掉所有为的项的数字个数成等差数列的特点可求得至第行结束，数列共有项，则第项为，从而加和可得结果.

    由题意可知，次二项式的二项式系数对应“杨辉三角”中的第行

    则“杨辉三角”第行各项之和为：

    第行去掉所有为的项的各项之和为：

    从第行开始每一行去掉所有为的项的数字个数为：

    则：，即至第行结束，数列共有项

    第项为第行第个不为的数，即为：

    前项的和为：

    本题正确结果：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】给出以下命题：

    ①双曲线的渐近线方程为y＝±x；

    ②命题p：“x∈R，sinx＋≥2”是真命题；

    ③已知线性回归方程为＝3＋2x，当变量x增加2个单位，其预报值平均增加4个单位；

    ④设随机变量ξ服从正态分布N(0,1)，若P(ξ>1)＝0.2，则P(－1<ξ<0)＝0.6；

    ⑤设，则

    则正确命题的序号为________(写出所有正确命题的序号)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数角度看，可以看成是以为自变量的函数，其定义域是.

    （1）证明：

    （2）试利用1的结论来证明：当为偶数时，的展开式最中间一项的二项式系数最大；当为奇数时的展开式最中间两项的二项式系数相等且最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（且）是定义在上的奇函数.

    （1）求的值；

    （2）求函数的值域；

    （3）当时， 恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，圆：与轴的一个交点为，圆的圆心为，为等边三角形.

    求抛物线的方程；

    设圆与抛物线交于两点，点为抛物线上介于两点之间的一点，设抛物线在点处的切线与圆交于两点，在圆上是否存在点，使得直线均为抛物线的切线，若存在求出点坐标（用表示）；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，．

    （1）设与相交于点，，且平面，求实数的值；

    （2）若且, 求二面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数（）的图象为， 关于点的对称的图象为， 对应的函数为．

    （Ⅰ）求函数的解析式，并确定其定义域；

    （Ⅱ）若直线与只有一个交点，求的值，并求出交点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面，，，，，是的中点．

    （1）求和平面所成的角的大小．

    （2）求二面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设，用表示不超过x的最大整数，则称为高斯函数，例如：，.已知函数，则关于函数的叙述中正确的是（ ）

    A.是偶函数B.是奇函数

    C.在R上是增函数D.的值域是

    E.的值域是

    查看答案和解析>>

    同步练习册答案