
【题目】已知点![]() ,且
,且![]() ,满足条件的
,满足条件的![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 两点,使得
两点,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() (2)存在,
(2)存在, ![]() 或
或![]() .
.
【解析】
(1)由![]() 得
得![]() 看成
看成![]() 到两定点
到两定点![]() 的和为定值,满足椭圆定义,用定义可解曲线
的和为定值,满足椭圆定义,用定义可解曲线![]() 的方程.
的方程.
(2)先讨论斜率不存在情况是否符合题意,当直线![]() 的斜率存在时,设直线点斜式方程
的斜率存在时,设直线点斜式方程![]() ,由
,由![]() ,可得
,可得![]() ,再直线与椭圆联解,利用根的判别式得到关于
,再直线与椭圆联解,利用根的判别式得到关于![]() 的一元二次方程求解.
的一元二次方程求解.
解:![]() 设
设![]() ,
,
由![]() ,
, ![]() ,
,
可得![]() ,即为
,即为![]() ,
,
由![]() ,可得
,可得![]() 的轨迹是以
的轨迹是以![]() 为焦点,且
为焦点,且![]() 的椭圆,
的椭圆,
由![]() ,可得
,可得![]() ,可得曲线
,可得曲线![]() 的方程为
的方程为![]() ;
;
![]() 假设存在过点
假设存在过点![]() 的直线l符合题意.
的直线l符合题意.
当直线![]() 的斜率不存在,设方程为
的斜率不存在,设方程为![]() ,可得
,可得![]() 为短轴的两个端点,
为短轴的两个端点,
![]() 不成立;
不成立;
当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() ,
,![]()
由![]() ,可得
,可得![]() ,即
,即![]() ,
,
可得 ,化为
,化为![]() ,
,
由![]() 可得
可得![]() ,
,
由![]() 在椭圆内,可得直线
在椭圆内,可得直线![]() 与椭圆相交,
与椭圆相交,
![]() ,
,
则![]()
化为![]() ,即为
,即为![]() ,解得
,解得![]() ,
,
所以存在直线![]() 符合题意,且方程为
符合题意,且方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形,![]()
![]() ,
,![]() 平面ABCD,E是棱PC上的一点.
平面ABCD,E是棱PC上的一点.
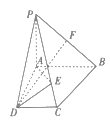
(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,F是PB的中点,
,F是PB的中点,![]() ,
,![]() ,求直线DF与平面
,求直线DF与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|,a∈R.
(1)当f(2)+f(﹣2)>4时,求a的取值范围;
(2)若a>0,x,y∈(﹣∞,a],不等式f(x)≤|y+3|+|y﹣a|恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体![]() 中,
中, ![]() 分别是
分别是![]() 的中点.则下述结论:
的中点.则下述结论:
①四面体![]() 的体积为
的体积为![]() ;
;
②异面直线![]() 所成角的正弦值为
所成角的正弦值为![]() ;
;
③四面体![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若用一个与直线![]() 垂直,且与四面体的每个面都相交的平面
垂直,且与四面体的每个面都相交的平面![]() 去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为
去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为![]() .
.
其中正确的有_____.(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 的图像上存在两个不同的点关于
的图像上存在两个不同的点关于![]() 轴对称,则称函数
轴对称,则称函数![]() 图像上存在一对“偶点”.
图像上存在一对“偶点”.
(1)写出函数![]() 图像上一对“偶点”的坐标;(不需写出过程)
图像上一对“偶点”的坐标;(不需写出过程)
(2)证明:函数![]() 图像上有且只有一对“偶点”;
图像上有且只有一对“偶点”;
(3)若函数![]() 图像上有且只有一对“偶点”,求
图像上有且只有一对“偶点”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月1日,济南轨道交通![]() 号线试运行,济南轨道交通集团面向广大市民开展“参观体验,征求意见”活动,市民可以通过济南地铁APP抢票,小陈抢到了三张体验票,准备从四位朋友小王,小张,小刘,小李中随机选择两位与自己一起去参加体验活动,则小王被选中的概率为( )
号线试运行,济南轨道交通集团面向广大市民开展“参观体验,征求意见”活动,市民可以通过济南地铁APP抢票,小陈抢到了三张体验票,准备从四位朋友小王,小张,小刘,小李中随机选择两位与自己一起去参加体验活动,则小王被选中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:
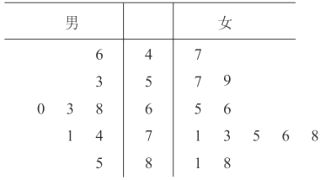
(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com