
分析 由已知$|\overrightarrow{a}|=2\sqrt{5}$,得m2+n2=20,再由$\overrightarrow{a}=λ\overrightarrow{b}$(λ<0)可知$\overrightarrow{a}$与$\overrightarrow{b}$共线反向,由此列式求得m,n的值,则答案可求.
解答 解:∵$\overrightarrow a=(m,n),\overrightarrow b=(1,-2)$,
∴由$|\overrightarrow a|=2\sqrt{5},\overrightarrow a=λ\overrightarrow b(λ<0)$,得
m2+n2=20,①
$\left\{\begin{array}{l}{m<0,n>0}\\{-2m-n=0}\end{array}\right.$,②
联立①②,解得m=-2,n=4.
∴m-n=-6.
故答案为:-6.
点评 本题考查平面向量的数量积运算,考查向量共线的坐标表示及向量模的求法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},\frac{1}{2})$ | B. | (-1,1) | C. | $(\frac{1}{2},-\frac{1}{2})$ | D. | (1,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
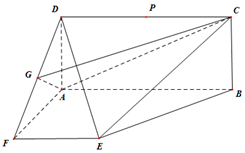 已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.
已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{3}}}{3}$ | B. | ±1 | C. | $±\sqrt{3}$ | D. | ±2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,0) | C. | (0,1) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ2+μ2=1 | B. | $\frac{1}{λ}$+$\frac{1}{μ}$=1 | C. | λ•μ=1 | D. | λ+μ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\sqrt{3},-1)$ | B. | $(-\sqrt{3},-1)$ | C. | $(-1,\sqrt{3})$ | D. | $(-1,-\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com