
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 边上的中线
边上的中线![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() .
.
(![]() )求
)求![]() 的顶点
的顶点![]() 、
、![]() 的坐标.
的坐标.
(![]() )若圆
)若圆![]() 经过不同的三点
经过不同的三点![]() 、
、![]() 、
、![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,求圆
,求圆![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:
(![]() )由题意可知直线
)由题意可知直线![]() 的方程为:
的方程为: ![]() ,与直线CD联立可得C点的坐标为
,与直线CD联立可得C点的坐标为![]() ,设
,设![]() ,则
,则![]() 的中点
的中点![]() ,代入方程
,代入方程![]() ,解得
,解得![]() ,所以
,所以![]() .
.
(![]() )由题意可得圆
)由题意可得圆![]() 的弦
的弦![]() 的中垂线方程为
的中垂线方程为![]() ,圆心
,圆心![]() 坐标为
坐标为![]() ,圆心
,圆心![]() 在直线
在直线![]() 上,则
上,则![]() ,且
,且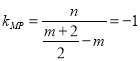 ,即
,即![]() ,据此可得圆心
,据此可得圆心![]() ,半径
,半径![]() ,所求圆方程为
,所求圆方程为![]() .
.
试题解析:
(![]() )
)![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() ,
,
所以直线![]() 的方程为:
的方程为: ![]() ,
,
又直线![]() 的方程为:
的方程为: ![]() ,
,
联立得![]() ,解得
,解得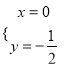 ,所以
,所以![]() ,
,
设![]() ,则
,则![]() 的中点
的中点![]() ,代入方程
,代入方程![]() ,
,
解得![]() ,所以
,所以![]() .
.
(![]() )由
)由![]() ,
, ![]() 可得,圆
可得,圆![]() 的弦
的弦![]() 的中垂线方程为
的中垂线方程为![]() ,
,
注意到![]() 也是圆
也是圆![]() 的弦,所以圆心在直线
的弦,所以圆心在直线![]() 上,
上,
设圆心![]() 坐标为
坐标为![]() ,
,
因为圆心![]() 在直线
在直线![]() 上,所以
上,所以![]() ①,
①,
又因为斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,所以
,所以![]() ,
,
即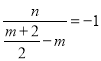 ,整理得
,整理得![]() ②,
②,
由①②解得![]() ,
, ![]() ,
,
所以圆心![]() ,半径
,半径![]() ,
,
故所求圆方程为![]() ,即
,即![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点;
是否过定点;
(3)若![]() 为圆
为圆![]() 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为![]() ,求四边形
,求四边形![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,上焦点
,上焦点![]() 到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=
到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=![]() .
.
(I)若P是椭圆C上任意一点,求![]() 的取值范围;
的取值范围;
(II)设过椭圆C的上顶点A的直线![]() 与椭圆交于点B(B不在y轴上),垂直于
与椭圆交于点B(B不在y轴上),垂直于![]() 的直线与
的直线与![]() 交于点M,与
交于点M,与![]() 轴交于点H,若
轴交于点H,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小萌大学毕业后,家里给了她10万元,她想办一个“萌萌”加工厂,根据市场调研,她得出了一组毛利润![]() (单位:万元)与投入成本
(单位:万元)与投入成本![]() (单位:万元)的数据如下:
(单位:万元)的数据如下:
投入成本 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 |
毛利润 | 1.06 | 1.25 | 2 | 3.25 | 5 | 7.25 | 9.98 |
为了预测不同投入成本情况下的利润,她想在两个模型![]() ,
,![]() 中选一个进行预测.
中选一个进行预测.
(1)根据投入成本2万元和4万元的两组数据分别求出两个模型的函数解析式,请你根据给定数据选出一个较好的函数模型进行预测(不必说明理由),并预测她投入8万元时的毛利润;
(2)若小萌准备最少投入2万元开办加工厂,请预测加工厂毛利润率![]() 的最大值,并说明理由.(
的最大值,并说明理由.(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】. (12分)如图所示,函数![]() 的一段图象过点
的一段图象过点![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得函数
个单位,得函数![]() 的图象,求函数
的图象,求函数![]() 的最大值,并求此时自变量
的最大值,并求此时自变量![]() 的取值集合.
的取值集合.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线y2=2px(p>0)焦点F的直线与抛物线交于A,B两点,作AC,BD垂直抛物线的准线l于C,D,其中O为坐标原点,则下列结论正确的是 . (填序号)
① ![]() ;
;
②存在λ∈R,使得 ![]() 成立;
成立;
③ ![]() =0;
=0;
④准线l上任意一点M,都使得 ![]() >0.
>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有标号为![]() ,
,![]() ,
,![]() 的
的![]() 个小球,其中标号
个小球,其中标号![]() 的小球有
的小球有![]() 个,标号
个,标号![]() 的小球有
的小球有![]() 个,标号
个,标号![]() 的小球有
的小球有![]() 个,现从口袋中随机摸出
个,现从口袋中随机摸出![]() 个小球.
个小球.
(![]() )求摸出
)求摸出![]() 个小球标号之和为偶数的概率.
个小球标号之和为偶数的概率.
(![]() )用
)用![]() 表示摸出
表示摸出![]() 个小球的标号之和,写出
个小球的标号之和,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com