
【题目】小萌大学毕业后,家里给了她10万元,她想办一个“萌萌”加工厂,根据市场调研,她得出了一组毛利润![]() (单位:万元)与投入成本
(单位:万元)与投入成本![]() (单位:万元)的数据如下:
(单位:万元)的数据如下:
投入成本 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 |
毛利润 | 1.06 | 1.25 | 2 | 3.25 | 5 | 7.25 | 9.98 |
为了预测不同投入成本情况下的利润,她想在两个模型![]() ,
,![]() 中选一个进行预测.
中选一个进行预测.
(1)根据投入成本2万元和4万元的两组数据分别求出两个模型的函数解析式,请你根据给定数据选出一个较好的函数模型进行预测(不必说明理由),并预测她投入8万元时的毛利润;
(2)若小萌准备最少投入2万元开办加工厂,请预测加工厂毛利润率![]() 的最大值,并说明理由.(
的最大值,并说明理由.(![]() )
)
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】为了节约用水,学校改革澡堂收费制度,实行计时收费,洗澡时间在30分钟以内(含30分钟),每分钟收费0.1元,30分钟以上超出的部分每分钟0.2元,请设计程序,使用基本语句完成澡堂计费工作,要求输入时间,输出费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内动点P与点A(﹣3,0)和点B(3,0)的连线的斜率之积为﹣ ![]() .
.
(1)求动点P的轨迹方程;
(2)设点P的轨迹且曲线C,过点(1,0)的直线与曲线C交于M,N两点,记△AMB的面积为S1 , △ANB的面积为S2 , 当S1﹣S2取得最大值时,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC, ![]() ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为 ![]() ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=
的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=![]() AB=1,点M在线段EC上.
AB=1,点M在线段EC上.
(Ⅰ)证明:平面BDM⊥平面ADEF;
(Ⅱ)判断点M的位置,使得三棱锥B﹣CDM的体积为![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 边上的中线
边上的中线![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() .
.
(![]() )求
)求![]() 的顶点
的顶点![]() 、
、![]() 的坐标.
的坐标.
(![]() )若圆
)若圆![]() 经过不同的三点
经过不同的三点![]() 、
、![]() 、
、![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
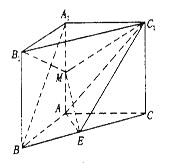
(Ⅰ)求证:A1B//平面AEC1;
(Ⅱ)在棱AA1上存在一点M,满足![]() ,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个对应f,不是从集合A到集合B的函数的是( ).
A. A=![]() ,B={-6,-3,1},
,B={-6,-3,1},![]() ,f (1)=-3,
,f (1)=-3,![]() ;
;
B. A=B={x|x≥-1},f (x)=2x+1;
C. A=B={1,2,3},f (x)=2x-1;
D. A=Z,B={-1,1},n为奇数时,f (n)=-1,n为偶数时,f (n)=1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com