
【题目】过抛物线y2=2px(p>0)焦点F的直线与抛物线交于A,B两点,作AC,BD垂直抛物线的准线l于C,D,其中O为坐标原点,则下列结论正确的是 . (填序号)
① ![]() ;
;
②存在λ∈R,使得 ![]() 成立;
成立;
③ ![]() =0;
=0;
④准线l上任意一点M,都使得 ![]() >0.
>0.
【答案】①②③
【解析】解:对于①,由 ![]() ,可得①正确;
,可得①正确;
对于②,设A(x1 , y1),B(x2 , y2),可得C(﹣ ![]() ,y1),D(﹣
,y1),D(﹣ ![]() ,y2),
,y2),
又kOA= ![]() =
= ![]() ,kAD=
,kAD= ![]() ,设直线AB方程为x=my+
,设直线AB方程为x=my+ ![]() .
.
代入抛物线的方程,可得y2﹣2pmy﹣p2=0,
可得y1y2=﹣p2 , 即有y1(y1﹣y2)=y12﹣y1y2=2px1+p2 ,
则kOA=kAD , 即有存在λ∈R,使得 ![]() 成立,则②正确;
成立,则②正确;
对于③, ![]() =(﹣p,y1)(﹣p,y2)=y1y2+p2=0,可得③正确;
=(﹣p,y1)(﹣p,y2)=y1y2+p2=0,可得③正确;
对于④,由抛物线的定义可得|AB|=|AC|+|BD|,
可得以AB为直径的圆的半径与梯形ACDB的中位线长相等,
即有该圆与CD相切,设切点为M,即有AM⊥BM,则 ![]() =0,
=0,
则④不正确.
所以答案是:①②③.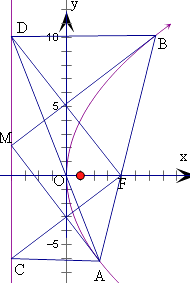


科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() ,
, ![]() 均为非零向量,已知命题p:
均为非零向量,已知命题p: ![]() =
= ![]() 是
是 ![]()
![]() =
= ![]()
![]() 的必要不充分条件,命题q:x>1是|x|>1成立的充分不必要条件,则下列命题是真命题的是( )
的必要不充分条件,命题q:x>1是|x|>1成立的充分不必要条件,则下列命题是真命题的是( )
A.p∧q
B.p∨q
C.(¬p)∧(¬q)
D.p∨(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC, ![]() ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为 ![]() ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=
的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=![]() AB=1,点M在线段EC上.
AB=1,点M在线段EC上.
(Ⅰ)证明:平面BDM⊥平面ADEF;
(Ⅱ)判断点M的位置,使得三棱锥B﹣CDM的体积为![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 边上的中线
边上的中线![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() .
.
(![]() )求
)求![]() 的顶点
的顶点![]() 、
、![]() 的坐标.
的坐标.
(![]() )若圆
)若圆![]() 经过不同的三点
经过不同的三点![]() 、
、![]() 、
、![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥O﹣ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.

(1)求异面直线BE与AC所成角的余弦值;
(2)求直线BE和平面ABC的所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
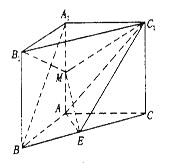
(Ⅰ)求证:A1B//平面AEC1;
(Ⅱ)在棱AA1上存在一点M,满足![]() ,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其30位亲属的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).

(1)根据茎叶图,帮助这位同学说明这30位亲属的饮食习惯.
(2)根据以上数据完成如下2×2列联表.

(3)能否有99%的把握认为其亲属的饮食习惯与年龄有关?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线l:2x+y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com