
分析 当n≥2根据题设条件可知an=2Sn-1,两式相减整理得an+1=3an,判断出此时数列{an}为等比数列,a2=2a1=4,公比为3,求得n≥2时的通项公式,最后综合可得答案.
解答 解:当n≥2时,an=2Sn-1,
∴an+1-an=2Sn-2Sn-1=2an,
即an+1=3an,
∴数列{an}为等比数列,a2=2a1=4,公比为3,
∴an=4•3n-2,
当n=1时,a1=2,
∴数列{an}的通项公式为:${a_n}=\left\{{\begin{array}{l}2\\{4×{3^{n-2}}}\end{array}}\right.\begin{array}{l}{n=1}\\{n≥2}\end{array}$.
故答案为:${a_n}=\left\{{\begin{array}{l}2\\{4×{3^{n-2}}}\end{array}}\right.\begin{array}{l}{n=1}\\{n≥2}\end{array}$.
点评 本题主要考查了数列的递推式求数列通项公式.解题的最后一定要验证a1.属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
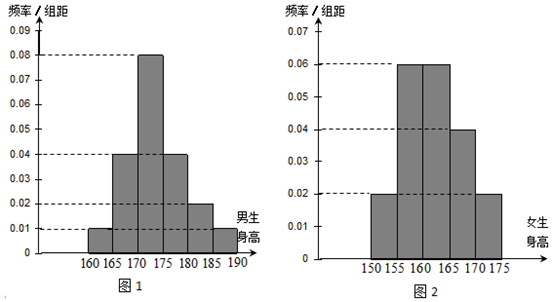
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
| P(K2≥k0) | 0.025 | 0.610 | 0.005 | 0.001 |
| k0 | 5.024 | 4.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com