
| ��170cm | ��170cm | �ܼ� | |
| �������� | |||
| ������ | |||
| �ܼ� |
| P��K2��k0�� | 0.025 | 0.610 | 0.005 | 0.001 |
| k0 | 5.024 | 4.635 | 7.879 | 10.828 |
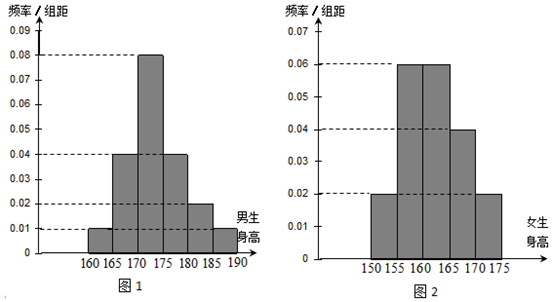
���� ��1������������Ů�����������2��2�������ж�Ӧ�����ݣ�����۲�ֵ�������ٽ�ֵ�ó����ۣ�
��2�����ֲ�����������������Ů�����������оٷ���������¼�������������ĸ���ֵ��
��� �⣺��1������������$\frac{16}{0.08��5}=40$��Ů��������80-40=40��
�������ߡ�170cm������=��0.08+0.04+0.02+0.01����5��40=30��
Ů�����ߡ�170cm������0.02��5��40=4��
���Կɵõ�����2��2��������
| ��170cm | ��170cm | �ܼ� | |
| �������� | 30 | 10 | 40 |
| ������ | 4 | 36 | 40 |
| �ܼ� | 34 | 46 | 80 |
���� ���⿼���˶����Լ�������оٷ���ŵ���͵ĸ������⣬���е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 6 | C�� | 10 | D�� | ��m�й� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?p���е������β��ǵ��������� | |
| B�� | ?p����������Dz����������� | |
| C�� | ?p�����е������ζ����ǵ��������� | |
| D�� | ?p�����е������ζ��ǵ��������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��1] | B�� | ��-�ޣ�-1]��[1��+�ޣ� | C�� | ��-1��1] | D�� | ��-�ޣ�-1����[1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2-2i | B�� | 2+2i | C�� | -2+2i | D�� | -2-2i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
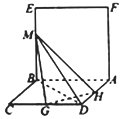 ��ͼ����֪ƽ��ABEF��ƽ��ABCD���ı���ABEF�������Σ��ı���ABCD�����Σ���BC=2����BAD=60�㣬��G��H�ֱ�Ϊ��CD��DA���е㣬��M���߶�BE�ϵĶ��㣮
��ͼ����֪ƽ��ABEF��ƽ��ABCD���ı���ABEF�������Σ��ı���ABCD�����Σ���BC=2����BAD=60�㣬��G��H�ֱ�Ϊ��CD��DA���е㣬��M���߶�BE�ϵĶ��㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com