练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知（x+1）10=a0+a1x+a2x2+…+a10x10，则（a0+a2+a4+a6+a8+a10）2-（a1+a3+a5+a7+a9）2的值为（　　）
    A．0B．1C．-1D．2

    分析 根据题意，令x=1，求出a0+a1+a2+…+a10的值，令x=-1，求出a0-a1+a2-a3+…-a9+a10的值，再因式分解后求值．

    解答 解：∵（x+1）10=a0+a1x+a2x2+…+a10x10，
    ∴当x=1时，210=a0+a1+a2+…+a10，
    x=-1时，0=a0-a1+a2-a3+…-a9+a10；
    ∴（a0+a2+a4+a6+a8+a10）2-（a1+a3+a5+a7+a9）2
    =（a0+a1+a2+a3+…+a9+a10）•（a0-a1+a2-a3+…-a9+a10）
    =210×0
    =0．
    故选：A．

    点评 本题考查了二项式定理的应用问题，也考查了用特殊值代入求值计算的问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

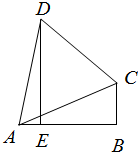    15．如图，在△ABC中，∠B为直角，DE⊥AB于E，AC⊥DC，设BC=1．
    （1）若∠BAC=30°，∠DAC=45°，试求△ADE的各边之长，由此推出75°的三角函数值；
    （2）设∠BAC=α，∠DAC=β（α、β，α+β均为锐角），试推出sin（α+β）的公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．如图，设甲地到乙地有4条路可走，乙地到丙地有5条路可走，那么由甲地经乙地到丙地，再由丙地经乙地到甲地，共有400种不同的走法．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若${∫}_{1}^{a}$（2x+$\frac{1}{x}$）dx=3+ln2且a＞1，则实数a的值是（　　）
    A．2B．3C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．若点（p，q），在|p|≤3，|q|≤3中按均匀分布出现，则方程x2+2px-q2+1=0有两个实数根的概率$\frac{36-π}{36}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．将四个编号为1，2，3，4的相同小球放入编号为1，2，3，4的四个盒子中，
    （1）若每个盒子放一个小球，求有多少种放法；
    （2）若每个盒子放一球，求恰有1个盒子的号码与小球的号码相同的放法种数；
    （3）求恰有一个空盒子的放法种数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若函数f（x）=x3-3x在区间（a，6-a2）上有最小值，则实数a的取值范围是[-2，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．在△ABC中内角A，B，C的对边分别为a，b，c，满足a=2，b=2$\sqrt{3}$，A=30°的△ABC的个数（　　）
    A．0B．1C．2D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知函数f（x）=|cosx|•sinx，给出下列四个说法：
    ①f（x）为奇函数；                    ②f（x）的一条对称轴为x=$\frac{π}{2}$；
    ③f（x）的最小正周期为π；             ④f（x）在区间[-$\frac{π}{4}$，$\frac{π}{4}$]上单调递增；
    ⑤f（x）的图象关于点（-$\frac{π}{2}$，0）成中心对称．
    其中正确说法的序号是①②④．

    查看答案和解析>>

    同步练习册答案