
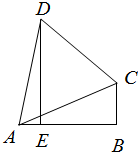 如图,在△ABC中,∠B为直角,DE⊥AB于E,AC⊥DC,设BC=1.
如图,在△ABC中,∠B为直角,DE⊥AB于E,AC⊥DC,设BC=1.分析 (1)由C向DE作垂线垂足为F,分别求得AD,AB和BE,进而求得AE和DE,最后求得答案.
(2)根据题意分别求得AC,AD,CD,DF,进而求得DE,最后求得答案.
解答 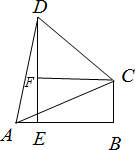 解:(1)由C向DE作垂线垂足为F,则CF=BE,∠CAB=∠FCA=30°,
解:(1)由C向DE作垂线垂足为F,则CF=BE,∠CAB=∠FCA=30°,
∴∠FCD=60°,∠DAE=30°+45°=75°,
根据题意AC=2BC=2=CD,AD=2$\sqrt{2}$,AB=$\sqrt{3}$
∴BE=CF=$\frac{1}{2}$CD=1,
∴AE=$\sqrt{3}$-1,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{8-4+2\sqrt{3}}$=$\sqrt{3}$+1,
∴sin75°=$\frac{DE}{AD}$=$\frac{\sqrt{3}+1}{2\sqrt{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,cos75°=$\frac{AE}{AD}$=$\frac{\sqrt{3}-1}{2\sqrt{2}}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
tan75°=$\frac{DE}{AE}$=$\frac{\sqrt{3}+1}{\sqrt{3}-1}$=2+$\sqrt{3}$
(2)由C向DE作垂线垂足为F,则CF=BE,∠CAB=∠FCA,$\frac{AC}{AD}$=cosβ,
则AC=$\frac{1}{sinα}$,$\frac{DC}{AC}$=tanβ,AD=$\frac{1}{sinαcosβ}$,
∴CD=AC•tanβ=$\frac{tanβ}{sinα}$,
DF=cosα•DC=$\frac{cosα•tanβ}{sinα}$,
∴DE=BC+DF=1+$\frac{cosα•tanβ}{sinα}$,
sin(α+β)=sin∠DAE=$\frac{DE}{AD}$=(1+$\frac{cosα•tanβ}{sinα}$)•sinαcosβ=sinαcosβ+cosαsinβ.
点评 本题主要考查了三角形中几何计算问题.考查了学生的观察能力和推理能力.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题

| A. | $\frac{{\sqrt{3}}}{3}c{m^3}$ | B. | $\frac{{4\sqrt{3}}}{3}c{m^3}$ | C. | $\frac{{8\sqrt{3}}}{3}c{m^3}$ | D. | $\sqrt{3}c{m^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{9}=1$ | B. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{9}$=1 | ||
| C. | $\frac{x^2}{9}-\frac{y^2}{9}=1$或$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{41}$-$\frac{{y}^{2}}{41}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
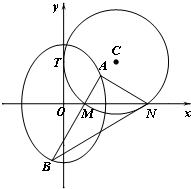 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com