
| A£® | 1 | B£® | 2 | C£® | 3 | D£® | 5 |
·ÖÎö ͨ¹ý½«$|\overrightarrow a+\overrightarrow b|=\sqrt{10}$¡¢$|\overrightarrow a-\overrightarrow b|=\sqrt{6}$Á½±ßƽ·½£¬ÀûÓÃ|$\overrightarrow{a}$|2=${\overrightarrow{a}}^{2}$£¬Ïà¼õ¼´µÃ½áÂÛ£®
½â´ð ½â£º¡ß$|\overrightarrow a+\overrightarrow b|=\sqrt{10}$£¬$|\overrightarrow a-\overrightarrow b|=\sqrt{6}$£¬
¡à£¨$\overrightarrow{a}$+$\overrightarrow{b}$£©2=10£¬£¨$\overrightarrow{a}$-$\overrightarrow{b}$£©2=6£¬
Á½ÕßÏà¼õµÃ£º4$\overrightarrow a$•$\overrightarrow b$=4£¬
¡à$\overrightarrow a$•$\overrightarrow b$=1£¬
¹ÊÑ¡£ºA£®
µãÆÀ ±¾Ì⿼²éÏòÁ¿ÊýÁ¿»ýÔËË㣬עÒâ½âÌâ·½·¨µÄ»ýÀÛ£¬ÊôÓÚ»ù´¡Ì⣮


 Ʒѧ˫ÓžíϵÁдð°¸
Ʒѧ˫ÓžíϵÁдð°¸ СѧÆÚÄ©³å´Ì100·ÖϵÁдð°¸
СѧÆÚÄ©³å´Ì100·ÖϵÁдð°¸ ÆÚÄ©¸´Ï°¼ì²âϵÁдð°¸
ÆÚÄ©¸´Ï°¼ì²âϵÁдð°¸ ³¬ÄÜѧµäµ¥ÔªÆÚÖÐÆÚĩרÌâ³å´Ì100·ÖϵÁдð°¸
³¬ÄÜѧµäµ¥ÔªÆÚÖÐÆÚĩרÌâ³å´Ì100·ÖϵÁдð°¸
| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | $\frac{1}{2}$ | B£® | $\frac{1}{4}$ | C£® | $\frac{1}{2e}$ | D£® | $\frac{1}{4e}$ |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
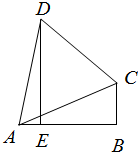 Èçͼ£¬ÔÚ¡÷ABCÖУ¬¡ÏBΪֱ½Ç£¬DE¡ÍABÓÚE£¬AC¡ÍDC£¬ÉèBC=1£®
Èçͼ£¬ÔÚ¡÷ABCÖУ¬¡ÏBΪֱ½Ç£¬DE¡ÍABÓÚE£¬AC¡ÍDC£¬ÉèBC=1£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | 2 | B£® | 3 | C£® | 5 | D£® | 6 |
²é¿´´ð°¸ºÍ½âÎö>>
¹ú¼ÊѧУÓÅÑ¡ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com