
分析 (Ⅰ)先求导,再分类讨论,根据导数和函数单调性的关系即可求出单调增区间;
(Ⅱ)函数f(x)在(-1,1)上有且只有一个极值点,等价于f′(x)在(-1,1)上有且只有一个解;由(II)及零点存在定理可得$\left\{{\begin{array}{l}{a<1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\{f'(-1)f'(1)<0}\end{array}}\right.$,从而可确定a的取值范围.
解答 解:(Ⅰ)因为f′(x)=x2-2(a+1)x+4a=(x-2a)(x-2),
令f′(x)=0,得x=2a或x=2.
当a>1时,f(x)的单调递增区间为(-∞,2),(2a,+∞);
当a=1时,f(x)的单调递增区间为(-∞,+∞);
当a<1时,f(x)的单调递增区间为(-∞,2a),(2,+∞).
(Ⅱ)由(Ⅰ)得f′(x)=x2-2(a+1)x+4a,
∵f(x)在(-1,1)内有且只有一个极值点,
∴$\left\{{\begin{array}{l}{a<1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\{f'(-1)f'(1)<0}\end{array}}\right.$,
解得-$\frac{1}{2}$<a<$\frac{1}{2}$.
所以a的取值范围是$({-\frac{1}{2},\frac{1}{2}})$.
点评 本题考查函数的极值和单调性的应用,解题的关键是对于字母系数a的讨论,注意讨论的过程中做到不重不漏,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$与y=x | B. | y=x0与y=1 | ||
| C. | y=2${\;}^{lo{g}_{4}x}$与y=$\frac{x}{\sqrt{x}}$ | D. | y=x与y=($\sqrt{x})^{2}$2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{9}=1$ | B. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{9}$=1 | ||
| C. | $\frac{x^2}{9}-\frac{y^2}{9}=1$或$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{41}$-$\frac{{y}^{2}}{41}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
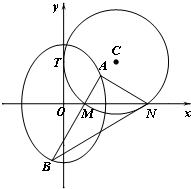 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(11,992).
把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(11,992).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com