
分析 (1)把四个编号为1,2,3,4的相同小球全排列即可,
(2)先确定一个1个盒子的号码与小球的号码相同,有4种,再确定,剩下的3个小球只有2种放法,根据分步计数原理可得.
(3)恰有一个空盒,则这4个盒子中只有3个盒子内有小球,且小球数只能是1、1、2.先从4个小球中任选2个放在一起,与其他两个球看成三个元素,在三个位置排列.
解答 解:(1)若每个盒子放一个小球,把四个编号为1,2,3,4的相同小球全排列,故有$A_4^4$=24种;
(2)假设1号小球放在1号盒子内,先放2号小球,若2号小球放在3号盒子里,则3号小球只能放在4号盒子里,4号小球只能放在2号盒子里,有1种方法,
若2号小球放在4号盒子里,则3号小球只能放在2号盒子里,4号小球只能放在3号盒子里,有1种方法,
故恰有1个盒子的号码与小球的号码相同的放法种$C_4^1•2$=8种;
(3)恰有一个空盒,则这4个盒子中只有3个盒子内有小球,
且小球数只能是1、1、2.
先从4个小球中任选2个放在一起,有C24种方法,
然后与其余2个小球看成三组,分别放入4个盒子中的3个盒子中,有A34种放法.
∴由分步计数原理知共有C24A34=144种不同的放法.
点评 本题考查计数问题,考查排列组合的实际应用,排列问题要做到不重不漏,有些题目带有一定的约束条件,解题时要先考虑有限制条件的元素,属于中档题.


科目:高中数学 来源: 题型:解答题
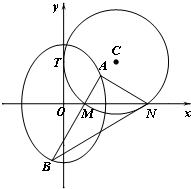 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(11,992).
把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(11,992).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1200 | B. | 1190 | C. | 1140 | D. | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com