
分析 (1)根据数列$\left\{{\left.{\frac{S_n}{n}}\right\}}$是公差为$\frac{a_1}{2}$的等差数列,即可得到an=na1,n∈N,问题得以解决;
(2)(i)根据递推关系式,求出${b_{4k-3}}+{b_{4k-2}}+{b_{4k-1}}+{b_{4k}}=7×{2^{4k-3}}$,即可求出数列{bn}的前4k项的和;
(ii)由题意得到,bn的表达式,利用作差法,以及分类讨论的思想即可证明.
解答 解(1):由题意,$\frac{S_n}{n}=\frac{S_1}{1}+(n-1)•\frac{a_1}{2}=\frac{n+1}{2}{a_1}$,
∴${S_n}=\frac{n(n+1)}{2}{a_1}$,
当n≥2时,${a_n}={S_n}-{S_{n-1}}=\frac{n(n+1)}{2}{a_1}-\frac{n(n-1)}{2}{a_1}=n{a_1}$,
当n=1时,上式也成立,
∴an=na1,n∈N*,
∵a1>0,
∴$\frac{a_6}{a_2}=\frac{{6{a_1}}}{{2{a_1}}}=3$.
(2)(ⅰ)由题意:${b_{n+1}}+{(-1)^n}{b_n}={2^n}$,
当k∈N*时,${b_{4k-2}}-{b_{4k-3}}={2^{4k-3}}$,${b_{4k-1}}+{b_{4k-2}}={2^{4k-2}}$,${b_{4k}}-{b_{4k-1}}={2^{4k-1}}$,
∴${b_{4k-3}}+{b_{4k-1}}={2^{4k-2}}-{2^{4k-3}}={2^{4k-3}}$,${b_{4k-2}}+{b_{4k}}={2^{4k-1}}+{2^{4k-2}}=3•{2^{4k-2}}$,
∴${b_{4k-3}}+{b_{4k-2}}+{b_{4k-1}}+{b_{4k}}=7×{2^{4k-3}}$,
∴前4k项的和T4k=(b1+b2+b3+b4)+(b5+b6+b7+b8)+…+(b4k-3+b4k-2+b4k-1+b4k)=$7×{2^1}+7×{2^5}+…+7×{2^{4k-3}}=\frac{{14({{16}^k}-1)}}{15}$.
(ⅱ)证明:由题意得:${b_{n+1}}+{b_n}={2^{n{a_1}}}={({2^{a_1}})^n}$,令$t={2^{a_1}}$,t∈(1,+∞),
∴$\frac{{{b_{n+1}}}}{{{{(-1)}^{n+1}}}}-\frac{b_n}{{{{(-1)}^n}}}=-{(-t)^n}$,
∴$\frac{b_n}{{{{(-1)}^n}}}=(\frac{b_n}{{{{(-1)}^n}}}-\frac{{{b_{n-1}}}}{{{{(-1)}^{n-1}}}})+(\frac{{{b_{n-1}}}}{{{{(-1)}^{n-1}}}}-\frac{{{b_{n-2}}}}{{{{(-1)}^{n-2}}}})+…+(\frac{b_2}{{{{(-1)}^2}}}-\frac{b_1}{{{{(-1)}^1}}})+\frac{b_1}{{{{(-1)}^1}}}$=$-[{(-t)^1}+{(-t)^2}+…+{(-t)^{n-1}}]-{b_1}=(\frac{t}{1-t}-{b_1})+\frac{{{{(-t)}^n}}}{1+t}$,
∴${b_n}=(\frac{t}{1+t}-{b_1}){(-1)^n}+\frac{t^n}{1+t}$,
∵bn+1>bn,n∈N*,
∴${b_{n+1}}-{b_n}=(\frac{t}{1+t}-{b_1}){(-1)^{n+1}}+\frac{{{t^{n+1}}}}{1+t}-(\frac{t}{1+t}-{b_1}){(-1)^n}-\frac{t^n}{1+t}$=$-2(\frac{t}{1+t}-{b_1}){(-1)^n}+\frac{t^n}{1+t}(t-1)>0$,
∴$({b_1}-\frac{t}{1+t}){(-1)^n}>\frac{{(1-t){t^n}}}{2(1+t)}$,n∈N*,
①当n为偶数时,${b_1}>\frac{{(1-t){t^n}}}{2(1+t)}+\frac{t}{1+t}$,
∵t∈(1,+∞),$\frac{{(1-t){t^n}}}{2(1+t)}+\frac{t}{1+t}≤\frac{{(1-t){t^2}}}{2(1+t)}+\frac{t}{1+t}=\frac{t(2-t)}{2}$,
∴${b_1}>\frac{t(2-t)}{2}$,
②当n为奇数时,${b_1}<\frac{{(t-1){t^n}}}{2(1+t)}+\frac{t}{1+t}$,
∵t∈(1,+∞),$\frac{{(t-1){t^n}}}{2(1+t)}+\frac{t}{1+t}≥\frac{{(t-1){t^1}}}{2(1+t)}+\frac{t}{1+t}=\frac{t}{2}$,
∴${b_1}<\frac{t}{2}$,
综上:$\frac{t(2-t)}{2}<{b_1}<\frac{t}{2}$,
即${2^{a_1}}-{2^{2{a_1}-1}}<{b_1}<{2^{{a_1}-1}}$.
点评 本题是数列与不等式的综合题,考查了等差数列与等比数列的性质和前n项和公式,考查了放缩法证明不等式以及分类讨论的思想,属于难题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:选择题
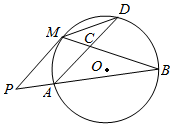 如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则MD等于( )
如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则MD等于( )| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{9}{4}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{π}{4}$,1) | B. | (2$\sqrt{2}$,$\frac{π}{4}$,1) | C. | (2,$\frac{5π}{4}$,1) | D. | (2$\sqrt{2}$,$\frac{5π}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 7 | C. | 5 | D. | $\frac{31}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com