
分析 (1)圆C的极坐标方程为C:$ρ=2\sqrt{2}sin(θ+\frac{π}{4})?{ρ^2}=2ρsinθ+2ρcosθ$,展开把x=ρcosθ,y=ρsinθ,代入即可得出直角坐标方程,利用cos2α+sin2α=1,即可得出参数方程.
(2)L:$ρsin(θ+\frac{π}{4})=4\sqrt{2}$,即$\frac{{\sqrt{2}}}{2}ρsinθ+\frac{{\sqrt{2}}}{2}ρcosθ=4\sqrt{2}$,把x=ρcosθ,y=ρsinθ代入可得直线的直角坐标方程,利用点到直线的距离公式可得圆心C到直线L的距离d,即可得出最小值d-r.
解答 解:(1)∵x=ρcosθ,y=ρsinθ,
C:$ρ=2\sqrt{2}sin(θ+\frac{π}{4})?{ρ^2}=2ρsinθ+2ρcosθ$,
化为普通方程是x2+y2=2y+2x?(x-1)2+(y-1)2=2.
所以圆C的参数方程是$\left\{\begin{array}{l}{x=1+\sqrt{2}cosα}\\{y=1+\sqrt{2}sinα}\end{array}\right.$(α为参数,0≤α≤2π).
(2)L:$ρsin(θ+\frac{π}{4})=4\sqrt{2}$,即$\frac{{\sqrt{2}}}{2}ρsinθ+\frac{{\sqrt{2}}}{2}ρcosθ=4\sqrt{2}$,
∵x=ρcosθ,y=ρsinθ,∴x+y-8=0.
则圆心C到直线L的距离为:$d=\frac{|1+1-8|}{{\sqrt{{1^2}+{1^2}}}}=3\sqrt{2}$,
∴M到直线L的距离的最小值为:$3\sqrt{2}-\sqrt{2}=2\sqrt{2}$.
点评 本题考查了极坐标与直角坐标方程的互化、圆的方程与直线方程的应用、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
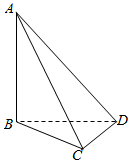 如图,在三棱锥A-BCD中,三条棱AB、BC、CD两两垂直,且AD与平面BCD成45°角,与平面ABC成30°角.
如图,在三棱锥A-BCD中,三条棱AB、BC、CD两两垂直,且AD与平面BCD成45°角,与平面ABC成30°角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
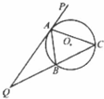 如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,使得QC2-QA2=BA•QC.
如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,使得QC2-QA2=BA•QC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
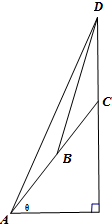 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD.为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进25m到达B处,又测得∠DBC=45°.根据以上数据计算可得cosθ=$\frac{\sqrt{3}-1}{2}$.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD.为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进25m到达B处,又测得∠DBC=45°.根据以上数据计算可得cosθ=$\frac{\sqrt{3}-1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图在底面为正方形,侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图在底面为正方形,侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6+2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 6 | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com